★ 北方工业大学电气与控制工程学院张尊栋，刘雨珂，刘小明

摘要：交通拥堵已经成为全世界范围内普遍存在的现象和亟待解决的难题，智能交通信号控制技术是缓解交通拥堵的重要手段。传统基于模型的自适应交通信号控制系统灵活性较低，往往依赖于大量的假设和经验方程，难以满足当前复杂多变交通系统的控制要求。随着计算机技术的进步、数据处理技术的发展和人工智能算法的成熟，结合深度强化学习方法的交通信号控制逐渐成为最主要的研究热点。 

1 引言

城市交通控制系统用于避免、减缓交通拥堵，在交叉口控制和主干路控制方面取得了很好的效果。随着城市规模的扩大和车辆保有量的增加，科研人员和工程师发现已有的控制方法难以实现整体的控制效果，交通拥堵问题日益突出^[1]。

随着人工智能技术的进步，交通系统正逐步朝着智能化方向发展。传统的自适应交通信号控制通过现有经验构建模型或简化的交通模型求解最优的信号控制策略，往往依赖于大量的假设和经验方程，难以满足当前复杂多变交通系统控制的要求。Mikam等人^[2]首次将强化学习用于交通信号控制。但强化学习方法在面对状态复杂、连续化问题时存在“维度爆炸”，而难以进行自主决策。伴随着强化学习和深度学习技术的发展，有学者提出将两者结合在一起形成深度强化学习方法（Deep Reinforcement Learning，DRL）^[3]。Li等人^[4]采用深度强化学习技术对单交叉口控制问题进行了研究，并作出了改进。由于强化学习及深度强化学习应用在普通简单路口的控制中往往能够取得较好效果，因此多交叉口交通信号控制越来越成为人们的研究热点。

本文将简述深度强化学习基础理论并根据动作选择方式对其分类，进而介绍深度强化学习方法在单交叉口、多交叉口交通信号控制领域的应用，最后讨论交通信号控制未来的研究方向和挑战。希望本篇综述能为研究深度强化学习在交通中的应用提供参考。

2 深度强化学习

深度学习强大的特征提取能力，结合强化学习的自主决策能力形成深度强化学习，使强化学习不再受数据空间维度问题，得以应用于高维、复杂的控制系统。根据优化过程中动作选取方式的不同，深度强化学习可以分为基于值的深度强化学习方法和基于策略梯度的深度强化学习方法。

2.1 基于值的深度强化学习方法

基于价值的深度强化学习方法通过准确估计状态-动作的价值函数，选取最大值所对应的动作，隐式获得确定性策略。采用深度神经网络对值函数或者动作值函数进行近似，将应用范围拓展到高维度问题和连续空间问题。Watkins等人^[5]提出的Q学习算法通过对Q值函数的估计，在当前状态下执行动作后转换到下一状态，智能体获取环境奖励并更新Q值函数。在有限的状态动作空间下，Q学习算法可以收敛到最优Q值函数。Mnih等人^[6]首次提出将深度神经网络与Q学习结合的DQN算法，利用卷积神经网络近似Q值，随后又提出利用目标网络和经验回放稳定DQN的学习过程^[3]。

然而，DQN每一次更新时都会采取最大化目标网络，导致对动作价值函数过估计问题。Hasselt等人^[7]采取双网络结构，当前网络选取最优动作，目标网络对所选动作进行评估，将动作选择与策略评价分离，降低发生过估计的可能性。Wang等人^[8]提出对抗架构DQN算法，直接估算状态值函数和动作优势函数，保证当前状态下各动作的优势函数相对排序不变，缩小Q值的范围同时去除多余的自由度，提高算法的稳定性。Nair等人^[9]提出了一个对于深度强化学习的大规模分布式架构，充分利用计算资源。此类算法只能处理有限的状态动作空间问题，难以应对复杂环境，学习过程中易出现过拟合且收敛性较差，因此其适用于离散动作空间下的深度强化学习过程。

2.2 基于策略梯度的深度强化学习方法

策略梯度算法使策略参数化，将神经网络的权重参数作为价值函数的参数，能通过分析所处的状态，直接输出下一步要采取的各种动作的概率，然后根据概率采取行动，每种动作都有相应的概率被选中。最经典的策略梯度算法REINFORCE^[10]使用蒙特卡洛方法计算状态值函数，近似替代策略梯度的价值函数。

由于蒙特卡洛策略梯度方法基于完整的经验更新值函数参数，导致模型的学习效率较低。在线学习的置信域策略优化算法TPRO^[11]与近端策略优化算法^[12]根据经验或自适应方法选择超参数，使得更新步长约束在一定范围内，确保持续获得更优策略，防止策略崩溃问题。

TPRO与PPO算法在每次策略更新时采样大量样本进行训练，需要大量算力确保算法收敛，导致其难以应用于大规模场景下的强化学习过程。Lillicrap^[13]提出深度确定性策略梯度算法DDPG，该方法使用非线性函数近似表示值函数，使得函数能够稳定收敛，解决了Q函数更新的发散问题。同时使用经验回放机制批处理学习，从而使训练过程更加稳定。Fujimoto等人^[14]为解决DDPG对于Q值的高估，及超参数和其他参数调整方面存在脆弱性的问题，提出TD3算法，可缓解动作价值高估的影响，并消除方差累计问题，使得训练过程波动较小，同时避免了DDPG中可能发生的特性故障。

与基于价值的深度强化学习方法相比，基于策略的强化学习方法具有更好的收敛性，特别在利用神经网络逼近函数时^[15]，它可以很容易地处理大量甚至连续的状态动作空间。但其缺点在于算法方差较高、收敛速度较慢及学习步长难以确定。

2.3 基于深度强化学习的交通信号控制模型设置

在基于深度强化学习的交通信号控制中，路网中的交通信号通常由一个智能体独立控制或多个智能体控制，智能体表示交通信号灯。智能体执行某动作后，环境会转换至一个新的状态，并根据状态的变化给出上一动作的奖励值，其控制框架如图1所示。深度强化学习的交通信号控制模型的关键问题是如何设置智能体，即奖励、状态和行动的定义^[16]。

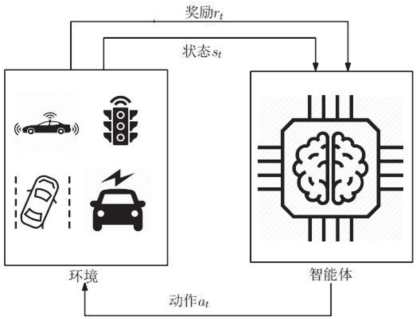
图1 深度强化学习控制框架

2.3.1 状态

智能体根据定量表示的环境状态决定采取的动作。常用状态可表示为描述环境的各种元素，如队列长度、等待时间、速度和相位等。这些元素可以在车道或路段上定义，进而连接为一个向量。在早期使用强化学习进行交通信号控制的工作中，人们需要离散状态空间，并使用一个简单的表格或线性模型来近似状态函数以提高效率^[17]。然而，现实世界的状态空间通常都很大，这在内存或性能方面限制了传统的强化学习方法。

随着深度学习的发展，深度强化学习方法被提出来作为一种有效的函数逼近器处理大的状态空间。Xu^[18]等人和Zhang^[19]等人将交叉口分割为固定长度的网格，通过每个网格中的布尔值确定该位置是否存在车辆，这种网络化的表示形式实现了交通状态编码的离散化，可以获得高分辨率的真实交叉口信息。一类广泛使用的状态定义方法将交叉口各个车道的特定信息的平均值或总值作为特征组成一个状态向量，例如车辆等待时间、排队长度及信号灯相位持续时间等^[20，21]。另一类使用图像来表示状态^[22，23]，其中车辆的位置被提取为图像表示。

2.3.2 动作

智能体在获得当前环境状态后，从动作集中选择要采取的动作并观察动作带来的奖励及新的环境状态。对交通信号控制的智能体有不同类型的动作定义：（1）设置当前相位持续时间^[24]；（2）设置当前相位持续时间与预定义的相位总周期持续时间的比率^[25]；（3）在预定义的信号配时方案中，由当前相位更改到下一相位，不改变相序^[26]；（4）在预定义的相位中选择需要更改的相位^[27]。动作的选择与交通信号的具体设置密切相关。例如，如果要求相位序列是循环的，那么应该考虑前三种作用方案，而在预定义的相位中选择需要更改的相位可以产生灵活的相位序列。

2.3.3 奖励

奖励反应深度强化学习智能体的学习目标，在交通信号控制中，考虑设置等待时间^[28，29]、累计延误^[30]及车辆排队长度^[31]等。单一的奖励难以全面反映环境反馈，因此一些学者考虑排队长度、等待时间等数据的权衡系数^[21]。然而奖励中每个因素的权重是难以设定的，而权重设置的微小差异可能会导致显著不同的结果^[32]。在面对多交叉口交通信号控制问题时，通常会设置全局奖励和局部奖励，局部奖励反映每个交叉口的交通状况，提高每个智能体的稳定性；而全局奖励使得智能体协作以学习整个路网的最优策略。在智能体的学习过程中，首先通过局部奖励关注局部任务，然后利用学习到的局部信息优化全局策略^[33]。

3 基于深度强化学习的单交叉口信号控制优化

近年来，基于深度强化学习的交通信号控制受到了研究者的广泛关注，由于其处理状态空间的能力，已经提出了许多深度强化学习模型进行信号控制。

利用深度神经网络近似Q函数^[34]，Gendes等人^[35]结合深度强化学习与交通信号控制，使用离散的交通状态编码模型，利用获取的交通环境信息来形成类似图像的状态表示。Gendes等人^[36]使用A3C算法研究了不同状态表示对信号控制优化的影响，并利用动态交通环境在单个十字路口上实验了三个独立的状态定义。其后，该作者研究了交通信号控制的异步深度强化学习模型，一般网络的全局参数在每隔n步后更新一次。与固定时间和驱动的交通控制器相比，提出的体系结构的性能提高了近40%。Garg等人^[37]提出了一种基于策略梯度的深度RL方法的自适应交通交叉口控制，该方法利用原始像素作为基于策略的DQN的输入状态。

Nishi等人^[38]提出了一种基于自动编码器的深度强化学习算法，通过将输入队列长度映射到低维动作集，考虑自动编码器进行动作选择。Gao等人^[39]提出了一种新的神经网络结构，神经网络的输出是二进制动作，无论是保持相同的动作还是在一个预定义的相位周期中改变动作。Choe等人^[40]在单交叉口信号控制场景中提出了一个基于RNN的DQN模型，与CNN结构相比该方法明显降低了旅行时间。Wan等人^[41]提出了一种基于新的折扣因子的动作值的DQN，他们所提出的动态折扣因子借助于无限几何级数，考虑了执行时间。Xu等人^[42]引入了一种新的具有批处理学习框架的迁移学习模型，利用相同的真实数据和一个合成的模拟数据在一个孤立的交叉口上进行实验。Jang等人^[43]通过java的AnyLogic多用途模拟器将DQN智能体与流量模拟器集成。

4 基于深度强化学习的多交叉口信号控制优化

4.1 基于博弈论的多智能体深度强化学习方法

博弈论是研究理性决策者之间策略交互的数学模型，是解决城市交通信号协调控制问题的合适方法，使控制策略能较好地适应交通需求水平的动态变化^[44，45]。近年来，结合博弈论的交通信号协调控制方法受到越来越多研究学者的重视。博弈论中的Nash均衡为路网中多个交叉口信号灯间的协调提供了理论框架，但仍面临着由于维度爆炸而难以向更多交叉口扩展的难题，且各交叉口存在重要程度的差异性，使得在交通优化过程中，次要交叉口会为重要交叉口牺牲通行能力，导致目标冲突问题^[46]。

目前，博弈论在交通领域中的应用大多集中在交通诱导和交通管理方面，而在交通信号配时决策中，博弈思想的应用还处于起步阶段^[47]。Clempner等人^[48]将多交叉口信号控制问题表述为Stackelberg博弈过程，基于超近距离方法采用纳什均衡求解。Zhao等人^[49]提出了一种基于协调博弈和Pareto最优的算法，仿真结果表明，该算法在平均排队长度、平均总延误和平均旅行时间方面比韦伯斯特配时法和驱动控制算法更有效。Zhu等人^[50]提出了一种基于行程数据的双层博弈方法来解决路网交通控制问题。多智能体系统的自学习、交互式等特点与城市路网的多交叉口结构上的相似性，引起了众多学者对多智能体系统及其自发学习机制在城市交通信号配时决策中应用的关注^[51]。在路网环境下，由于系统中对任一交叉口信号灯的控制可能将延误传导至上下游以及其他交叉口^[50]，在此环境中的信号灯智能体的行为对环境的改变也会影响到其他智能体^[52]。因此，与均衡相关的混合型博弈MARL算法^[53]适用于路网信号控制问题。

近年来，许多研究者通过将MARL与博弈论相结合，使用博弈中的均衡解代替最优解，以求得相对有效且合理的交通信号控制策略^[54]。Abdoos等人^[54]提出了一种双模式智能体结构，通过独立和协作的过程有效地控制交通拥塞问题。在协作模式中，利用博弈论来确定智能体之间的协作机制，动态控制多个交叉口的交通信号。Guo等人^[55]将博弈论与强化学习（RL）中的Q学习算法进行结合，提出了面向单交叉口信号灯的半合作NashQ学习算法和半合作StackelbergQ学习算法。Pan等人^[56]融入博弈论的混合策略Nash均衡概念，改进IA-MARL算法的决策过程，提出了考虑博弈的多智能体强化学习（G-MARL）框架。Zhang等人^[57]提出了基于Nash均衡的多智能体深度强化学习算法。Camponogara^[58]利用随机博弈论和RL研究了两个交叉口信号灯之间的协调问题。Abolghasem^[59]采用模糊Q学习和博弈论的方法，智能体根据以往经验和相邻智能体的策略进行决策。

4.2 平均场多智能体深度强化学习方法

通过平均场相互作用来描述大量具有对称相互作用且不可区分参与者的行为。每个智能体都被表示为网格中的一个节点，该节点只受其邻居的平均效应的影响。多智能体相互作用被有效地转换为两个智能体间相互作用。根据代理所试图实现的目标，可以分成平均场博弈（MFG）和平均场控制（MFC）两种类型的平均场问题。

对于MFC，分析了大种群中合作博弈的最优解，Gu等人^[60]提出了MFC与Q函数结合的IQ函数，通过将状态-空间替换为概率分布空间来提升强化学习。Carmona等人^[61]基于MFC突出一个通用的强化学习框架，在此基础上实现了基于状态-动作值函数的通用无模型算法。

MFG的目的是在非合作的多玩家博弈中寻找纳什均衡，由Lasry等人^[62]和Huang等人^[63]提出，以模拟相互作用中大量相同代理之间的动态平衡，试图克服多智能体博弈问题中纳什均衡所出现的困难。这类系统包括许多应用程序的建模，如交通堵塞动态、群体系统、金融市场均衡、人群疏散、智能电网控制、网络广告拍卖、疫苗接种动态等。Yang等人^[64]证明了特殊的MFG可简化为马尔可夫决策过程（MDP），实现了MFG和MDP的结合，从而拓宽MFG的范围，并通过深度逆强化学习来推断大型现实世界系统的MFG模型。Xin等人^[65]定义了一个基于模拟器的Q学习算法以求解有限状态和动作空间下的平均场博弈。Anahtarc等人^[66]证明了正则化Q学习在有限状态和动作空间下的收敛性。Fu等人^[67]提出了线性函数逼近的平均场演员评论家算法，并证明该算法以线性速率收敛到纳什均衡。

将平均场理论与MARL结合，Blume等人^[68]将每个智能体只与一组有限的邻居直接交互，任意两个智能体间通过有限的直接交互链间接交互，在降低智能体间相互作用复杂性的同时，仍保留了任何一对智能体之间的全局相互作用。Stanley等人^[69]采用平均场理论逼近成对智能体间的相互影响。Lasry等人^[62]利用平均场论将多智能体环境中的相互作用近似为两个智能体相互作用。Yang等人^[70]采用平均场理论，将多智能体间的相互作用近似为单个主体与整个总体或相邻主体的平均效应之间的相互作用，利用离散时间平均场博弈来理解个体行为的总体效应，并预测种群分布的时间演化。Hu等人^[71]设置一个智能体数量接近无限大的多智能体系统，通过平均效应来近似其他智能体对单个智能体的影响，导出描述多智能体群体中Q值概率分布演变的Fokker-Planck方程。Subramanian等人^[72]提出一种基于策略梯度的方法来实现平均场均衡。

深度神经网络具有强大的泛化能力，已被广泛应用于直接逼近策略或值函数。利用神经网络作为函数逼近器，可以解决MARL中的非平稳问题。Yang等人^[70]提出了MF-Q及MF-AC算法，分析得到了Nash均衡的一致性，并在高斯挤压、伊辛模型和战斗游戏的实验中证明了算法学习效果。该方法降低相互作用复杂性的同时，仍保留了任何一对智能体之间的全局相互作用，解决了维度爆炸问题，降低了环境的非平稳性。

4.3 联网自动车辆环境下的多智能体深度强化学习方法

传感、通信、网络和计算技术的快速发展引发了新兴的概念，如联网自动车辆（CAV）。在CAV的范式中，未来的车辆可以通过大量的车载设备有效地监测其内部健康状况，以提高运输安全。此外，车辆将变得更加智能，能够完全自主驾驶，极大地改善了用户体验。DRL智能体通过与环交互，通过反复错来学习正确的操作。这样，基于深度强化学习的模型就不会受到人类行为的限制，从而产生一些超人的行为。

此外，CAV还可以通过与环境的交互来体验数字交通条件。当采取不当行动时，它们可能会产生或遇到一些角落的场景，如碰撞和近碰撞。通过这种方式，它们将受到惩罚，从而学会避免危险或容易崩溃的行为。因此，学习到的基于深度强化学习的模型通常承诺具有鲁棒性。深度强化学习已成功应用于许多CAV控制任务，如车道保持、车道改变、避障、合并和交叉。新兴的CAV技术为城市信号交叉口管理提供了新的机会。通过无线通信和先进的传感能力，CAV可以检测周围的交通环境，与基础设施实时共享车辆信息，可以精确控制CAV的各个轨迹。

之前的一些研究已经将CAV数据纳入交通信号控制，并检查了由此产生的好处^[73]。Lee等人^[74]开发了一种在100%CAV市场渗透率（MPR）下的累积旅行时间响应式实时交叉口控制算法，其中总延迟可减少34%。Guler等人^[75]整合了来自简历和检测器的信息，优化了双向交叉口的放电序列，在平衡交通需求的情况下，减少了55%的平均延迟。Feng等人^[76]提出了一个利用CAV轨迹信息来支持交通信号优化的双层优化框架，并采用动态规划（DP）来解决该问题。他们还提出了一种估计未装备车辆的速度和位置的算法。结果表明，在100%PR下，不同目标函数下的平均延迟可以从6.37%降低到16.33%。Li和Ban^[77]还提出了一种两阶段信号优化方法，它可以很容易地扩展到多个信号的协调。

另一个研究方向是根据实时信号相位和定时（SPaT）和交通条件完全控制CAV轨迹^[78，79]。我们开发了一些基于CAV的模型/算法来控制个体车辆轨迹^[80-82]，其中CAV可以根据给定的SPaT调整其轨迹。一些研究采用传统方法获取最优轨迹，如模型预测控制^[83，84]、DP^[85，86]和近似模型^[87，88]。然而，这些模型/算法中的大多数都是计算密集型的。因此，提出了具有给定边界的分析方法，以减少计算负担^[89，90]。Zhoou等人^[91]提出了一种简约的启发式算法，该算法通过控制详细的加速度剖面，可以有效地平滑接近信号交叉口的车辆流的所有轨迹。该算法用几段解析二次曲线来表示每一个无限维的车辆轨迹。因此，它有效地构建了大量的车辆轨迹，受物理限制、车辆跟踪安全和交通信号定时。

最近，研究者关注了信号优化和车辆轨迹控制的集成框架——这是继简历和汽车文献之后自然的下一步。然而，据我们所知关于这一主题的研究数量仍然有限。Li等人^[92]早期研究信号和车辆轨迹的联合控制，使用简单的运动学构建车辆轨迹，同时纯粹列举最优信号规划。Pourmehrab等人^[93]继续这项研究，用绿色时间延长取代了纯计数，没有考虑车辆和信号定时控制之间的复杂相互作用。Feng等人^[94]提出了一个时空交通控制框架来优化交通信号和车辆轨迹。Yu等人^[95]联合优化了100%CAV场景下的交通信号和车辆轨迹，其中考虑了所有车辆的运动，包括左转、右转弯和通过交通。索利曼亚米里等人^[96]提出了一种使用简化近似函数的解析联合优化方法，结果显示在两相交叉处有显著的改进。

5 总结与展望

本文针对深度强化学习在交通信号控制中的应用进行了总结，许多研究到目前为止获得了卓越的研究成果，但仍存在许多重大挑战和亟待解决的技术问题。下面对未来的研究方向进行探讨。

5.1 协调

在多交叉口信号控制中需要协调智能体使其共识达成一致，特别是，在合作环境中实现共同目标需要连贯的动作选择，以便联合动作实现共同优化目标。在决策过程中找到共识可以通过智能体之间的信息交换实现，也可以通过构建模型实现。前者需要智能体通信机制，以便智能体可在各自目标的基础上进行协调。对于后者，智能体需要能够观察其他智能体的动作并推理其策略以构建模型。在预测模型基础上，智能体可以学习其他智能体的动作模式，并将动作应用到共识中从而实现协调。

5.2 可计算性

对大量智能体进行训练的难度非常大，环境中的每个智能体都会给学习过程增加额外的复杂性，从而使计算量因智能体数量呈指数级增长。除了复杂性问题之外，众多可变因素也使得智能体需要对其他智能体的行为具有鲁棒性。但是，智能体可以利用智能体之间共享的分布式知识来加速学习过程。

5.3 安全性

未来研究工作还集中在安全性方面，安全性是非常重要的属性，因为自主智能体要确保交通系统性能，同时还要在学习和执行动作期间确保安全。单智能体学习算法研究中涉及了安全概念，但其对多智能体学习的适用性有限，仍处于起步阶段。

综上所述，基于深度强化学习的多交叉口信号控制优化是研究领域现阶段研究的难点与重点之一，每个智能体都有一个需要优化的本地目标，然而，只有当智能体允许其他智能体能成功完成其任务时，才能实现全局最优。另一个可能方向是深度多智能体强化学习算法和进化方法之间的融合。进化算法已被用于多智能体强化学习的环境中，由于进化需要许多实体进行适应，因此多智能体强化学习场景非常适合进化计算。

现阶段大多数研究都集中在同质环境中的学习，在这些环境中智能体具有共同的兴趣并优化共同的目标。当智能体具有共同利益时，诸如非平稳性、部分可观察性和协调性之类的问题可能会减少。然而，异质性意味着智能体可能有自己的兴趣和目标，个人经验和知识，或者不同的技能和能力。在真实应用场景中，智能体需要利用异构信息做出决策。

随着交叉口数量的增加，基于深度强化学习的交通信号控制优化领域最根本问题是维度灾难，“状态-动作”空间和智能体相互作用的组合随着智能体数量呈指数级增长，这使得完全遍历空间难以实现。且当智能体只能获得对环境的部分观察或当环境具有连续性质时，这种情况会加剧。尽管深度神经网络作为函数近似器可以应对连续空间，并且可以很好地降低计算量，但仍然存在一些问题，比如如何充分探索大型和复杂路网，以及如何解决区域交通信号优化问题等。

作者简介:

张尊栋（1979-），男，讲师，博士，现任教于北方工业大学，研究方向为智能交通。

刘雨珂（1999-），女，硕士，现就读于北方工业大学，研究方向为智能交通。

刘小明（1974-），男，教授，博士，现任教于北方工业大学，研究方向为交通流理论、智能交通控制。

参考文献：

[1] WEIH, ZHENG G, GAYAH V, et al. Recent advances in reinforcement learning for traffffic signal control: A survey of models and evaluation[J]. SIGKDD Explor. Newsl., 2021, 22 (2) : 12 - 18.

[2] MIKAMI S, KAKAZU Y. Genetic reinforcement learning for cooperative traffffic signal control[C]//Proceedings of the First IEEE Conference on Evolutionary Computation. IEEE World Congress on Computational Intelligence. [S.l.: s.n.], 1994 : 223 - 228 vol.1.

[3] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518 : 529 - 533.

[4] LI L, LV Y, WANG F Y. Traffffic signal timing via deep reinforcement learning[J]. IEEE/CAA Journal of Automatica Sinica, 2016, 3 (3) : 247 - 254.

[5] WATKINS J, DAYAN P. Q-learning[J]. Machine Learning, 1992, 8 : 279 -292.

[6] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning[J]. Computer Science, 2013.

[7] VAN HASSELT H, GUEZ A, SILVER D. Deep reinforcement learning with double q-learning[Z]. [S.l.: s.n.], 2016.

[8] WANG Z, SCHAUL T, HESSEL M, et al. Dueling network architectures for deep reinforcement learning[C]//ICML'16: Proceedings of the 33rd International Conference on International Conference on Machine Learning - Volume 48. [S.l.]: JMLR.org, 2016 : 1995 - 2003.

[9] NAIR A, SRINIVASAN P, BLACKWELL S, et al. Massively parallel methods for deep reinforcement learning[J]. Computer Science, 2015.

[10] WILLIAMS R J. Simple statistical gradient-following algorithms for connectionist reinforcement learning[J]. Machine Learning, 1992, 8 (3- 4) : 229 - 256.

[11] SCHULMAN J, LEVINE S, ABBEEL P, et al. Trust region policy optimization[C]//Proceedings of Machine Learning Research: volume 37 Proceedings of the 32nd International Conference on Machine Learning. [S.l.]: PMLR, 2015 : 1889 - 1897.

[12] SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[J]. Advances in Neural Information Processing Systems, 2017.

[13] LILLICRAP T, HUNT J, PRITZEL A, et al. Continuous control with deep reinforcement learning[J]. CoRR, 2015 : 09.

[14] FUJIMOTO S, VAN HOOF H, MEGER D. Addressing function approximation error in actorcritic methods[J]. ArXiv, 2018, abs/1802.09477.

[15] LIU B, CAI Q, YANG Z, et al. Neural proximal/trust region policy optimization attains globally optimal policy[M]. [S.l.]: Curran Associates Inc., 2019.

[16] YAU K L A, QADIR J, KHOO H L, et al. A survey on reinforcement learning models and algorithms for traffffic signal control[J]. ACM Comput. Surv., 2017, 50 (3) .

[17] ABDOOS M, MOZAYANI N, BAZZAN A L C. Hierarchical control of traffffic signals using q-learning with tile coding[J]. Applied Intelligence, 2013, 40 : 201 - 213.

[18] XU M, WU J, HUANG L, et al. Network-wide traffffic signal control based on the discovery of critical nodes and deep reinforcement learning[J]. Journal of Intelligent Transportation Systems, 2020, 24 (1) : 1 - 10.

[19] ZHANG R, ISHIKAWA A, WANG W, et al. Using reinforcement learning with partial vehicle detection for intelligent traffffic signal control[J/OL]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22 (1) : 404 - 415.

[20] CHU T, WANG J, CODECà L, et al. Multi-Agent Deep Reinforcement Learning for Large-Scale Traffffic Signal Control[J/OL]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21 (3) : 1086 - 1095.

[21] XIE D, WANG Z, CHEN C, et al. Iedqn: Information exchange dqn with a centralized coordinator for traffffic signal control[C/OL]//2020 International Joint Conference on Neural Networks (IJCNN) . 2020 : 1 - 8.

[22] LIANG X, DU X, WANG G, et al. A deep reinforcement learning network for traffffic light cycle control[J/OL]. IEEE Transactions on Vehicular Technology, 2019, 68 (2) : 1243 - 1253.

[23] GONG Y, ABDEL-ATY M, CAI Q, et al. Decentralized network level adaptive signal control by multi-agent deep reinforcement learning[J/OL]. Transportation Research Interdisciplinary Perspectives, 1 : 100020.

[24] ASLANI M, SEIPEL S, MESGARI M S, et al. Traffffic signal optimization through discrete and continuous reinforcement learning with robustness analysis in downtown tehran[J/OL]. Advanced Engineering Informatics, 2018, 38 : 639-655. https://www.sciencedirect.com/scienc e/article/pii/S1474034617302598.

[25] MA Z, CUI T, DENG W, et al. Adaptive optimization of traffffic signal timing via deep reinforcement learning[J/OL]. Journal of Advanced Transportation, 2021, 2021 : 1 - 14.

[26] ZHU Y, CAI M, SCHWARZ C, et al. Intelligent traffffic light via policy- based deep reinforcement learning[J]. International Journal of Intelligent Transportation Systems Research, 2021, 20 : 734 - 744.

[27] SUN Y, LAI J, CAO L, et al. A Friend-or-Foe framework for multi-agent reinforcement learning policy generation in mixing cooperative– competitive scenarios[J]. Transactions of the Institute of Measurement and Control, 2022, 44 : 2378 - 2395.

[28] LI D, WU J, XU M, et al. Adaptive traffffic signal control model on intersections based on deep reinforcement learning[J]. Journal of Ad vanced Transportation, 2020, 2020 : 1 - 14.

[29] SHABESTARY S M A, ABDULHAI B. Adaptive traffffic signal control with deep reinforcement learning and high dimensional sensory inputs: Case study and comprehensive sensitivity analyses[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23 : 20021 - 20035.

[30] GUILLEN-PEREZ A, CANO M D. Intelligent iot systems for traffffic management: A practical application[J]. IET Intelligent Transport Systems, 2021.

[31] WU T, ZHOU P, LIU K, et al. Multi-agentdeep reinforcement learning for urban traffffic light control in vehicular networks[J]. IEEE Transactions on Vehicular Technology, 2020, 69 : 8243 - 8256.

[32] BOUKERCHE A F M, ZHONG D, SUN P. A novel reinforcement learning-based cooperative traffffic signal system through max pressure control[J]. IEEE Transactions on Vehicular Technology, 2021, 71 : 1187 - 1198.

[33] SAKIB S M N, TAZRIN T, FOUDA M M, et al. An efffficient and lightweight predictive channel assignment scheme for multiband b5g- enabled massive iot: A deep learning approach[J]. IEEE Internet of Things Journal, 2021, 8 : 5285 - 5297.

[34] AREL I, LIU C, URBANIK T, et al. Reinforcement learning-based multi- agentsystem for network traffffic signal control[J]. Iet Intelligent Transport Systems, 2010, 4 : 128 - 135.

[35] GENDERS W, RAZAVI S N. Using a deep reinforcement learning agent for traffffic signal control[J]. ArXiv, 2016, abs/1611.01142.

[36] GENDERS W, RAZAVI S. Evaluating reinforcement learning state representations for adaptive traffffic signal control[J]. Procedia Computer Science, 2018, 130 : 26 - 33.

[37] GARG D, CHLI M, VOGIATZIS G. Deep reinforcement learning for autonomous traffffic light control[C/OL]//2018 3rd IEEE International Conference on Intelligent Transportation Engineering (ICITE) . 2018 : 214 - 218.

[38] NISHI T, OTAKI K, HAYAKAWA K, et al. Traffffic signal control based on reinforcement learning with graph convolutional neural nets[C/OL]//2018 21st International Conference on Intelligent Transportation Systems (ITSC) . 2018 : 877 - 883.

[39] GAO J, SHEN Y, LIU J, et al. Adaptive traffffic signal control: Deep reinforcement learning algorithm with experience replay and target network[J]. ArXiv, 2017, abs/1705.02755.

[40] CHOE C J, BAEK S, WOON B, et al. Deep q learning with lstm for traffffic light control[C/OL]//2018 24th Asia-Pacific Conference on Communications (APCC) . 2018 : 331 - 336.

[41] WAN C H, HWANG M C. Value-based deep reinforcement learning for adaptive isolated intersection signal control[J/OL]. IET Intelligent Transport Systems, 2018, 12 : 1005 - 1010.

[42] XU N, ZHENG G, XU K, et al. Targeted knowledge transfer for learning traffffic signal plans[C]//Pacific-Asia Conference on Knowledge Discovery and Data Mining. [S.l.: s.n.], 2019.

[43] JANG I, KIM D, LEE D, et al . An agent -based simulation model ing with deep reinforcement learning for smart traffffic signal control[C/OL]//2018 International Conference on Information and Com munication Technology Convergence (ICTC) . 2018 : 1028 - 1030.

[44] Nam Bui K H, JUNG J J. Cooperative game-theoretic approach to traffffic flow optimization for multiple intersections[J].Computers and Electrical Engineering, 2018, 71 : 1012 - 1024.

[45] ARAGON-GóMEZ R, CLEMPNER J B. Traffffic-signal control reinforcement learning approach for continuous-time markov games[J]. Engineering Applications of Artificial Intelligence, 2020, 89 : 103415.

[46] RUI T, CHAI L, SHANGGUAN W, et al. Multi mode travel recom mendation method for passengers at hub airport under the

constraint of public transport timetable[C]//2021 China Automation Congress (CAC) . [S.l.: s.n.], 2021 : 6106 - 6112.

[47] KYAMAKYA K, CHEDJOU J C, AL-MACHOT F, et al. Intelligent transportation related complex systems and sensors[J]. Sensors, 2021, 21 (6) .

[48] CLEMPNER J B, POZNYAK A S. Modeling the multi-traffffic signal- control synchronization: A markov chains game theory approach[J]. Engineering Applications of Artificial Intelligence, 2015, 43 : 147 - 156.

[49] ZHAO Y, LIANG Y, HU J, et al. Traffffic signal control for isolated intersection based on coordination game and pareto efffficiency[C]//2019 IEEE Intelligent Transportation Systems Conference (ITSC) . [S.l.: s.n.], 2019 : 3508 - 3513.

[50] ZHU Y, HE Z, LI G. A bi-hierarchical game-theoretic approach for network-wide traffffic signal control using trip-based data[J/OL]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23 (9) : 15408 - 15419.

[51] CHEN C, WEI H, XU N, et al. Toward a thousand lights: Decentralized deep reinforcement learning for large-scale traffffic signal control[C]// AAAI 2020 - 34th AAAI Conference on Artificial Intelligence: AAAI 2020 - 34th AAAI Conference on Artificial Intelligence.

[S.l.]: AAAI press, 2020 : 3414 - 3421.

[52] BU ONIU L, BABUš KA R, DE SCHUTTER B. Multi- Agent Reinforcement Learning: An Overview[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010 : 183 - 221.

[53] GRONAUER S, DIEPOLD K. Multi-agent deep reinforcement learning: a survey[J]. Artificial Intelligence Review, 2021, 55 : 895 - 943.

[54] ABDOOS M. A Cooperative Multi agent system for traffffic signal control using game theory and reinforcement learning[J/OL].IEEE Intelligent Transportation Systems Magazine, 2021, 13 (4) : 6 - 16.

[55] GUO J, HARMATI I. Evaluating semi-cooperative nash/stackelberg q-learning for traffffic routes plan in a single intersection[J]. Control Engineering Practice, 2020, 102 : 104525.

[56] PAN Z, QU Z, CHEN Y, et al. A distributed assignment method for dy namic traffffic assignment using heterogeneous-adviser based multi-agent reinforcement learning[J/OL]. IEEE Access, 2020, 8 : 154237 - 154255.

[57] ZHANG Z, QIAN J, FANG C, et al . Coordinated control of distributed traffffic signal based on multi agent cooperative game[J/OL]. Wireless communications and mobile computing, 2021, 2021 : 1 - 13.

[58] CAMPONOGARA E, KRAUS W. Distributed learning agents in urban traffffic control[C]//PIRES F M, ABREU S. Progress in Artifi-cial Intelligence. Berlin, Heidelberg: Springer Berlin Heidelberg, 2003 : 324 - 335.

[59] DAEICHIAN A, HAGHANI A. Fuzzy q-learning-based multi-agent system for intelligent traffffic control by a game theory approach[J]. Arabian journal for science and engineering, 2018, 43 : 3241 - 3247.

[60] GU H, GUO X, WEI X, et al. Dynamic programming principles for meanfield controls with learning[J]. arXiv, 2019.

[61] CARMONA R, LAURIèRE M, TAN Z. Model-free mean-field re inforcement learning: Mean-field mdp and mean-field q-learning[J]. arXiv, 2019.

[62] LASRY J M, LIONS P L. Mean field games[J]. Japanese journal of mathematics, 2007, 2 (1) : 229 - 260.

[63] HUANG M, MALHAME R, CAINES P. Large population stochastic dynamic games: Closed-loop mckean-vlasov systems and the nash certainty equivalence principle[J]. Commun. Inf. Syst., 2006, 6.

[64] YANG J, YE X, TRIVEDI R, et al. Deep mean field games for learning optimal behavior policy of large populations[C]// International confer ence on learning representations. [S.l.: s.n.], 2018.

[65] GUO X, HU A, XU R, et al. Learning mean-field games[J]. In Advances in Neural Information Processing Systems, 2019: 4966-4976.

[66] ANAHTARCL B, KARIKSIZ C, SALDI N. Q-learning in regularized mean-field games[J]. arXiv, 2020.

[67] FU Z, YANG Z, CHEN Y, et al. Actorcritic provably finds nash equilibria of linear-quadratic mean-field games[J]. CoRR, 2019,abs/1910.07498.

[68] BLUME L E. The statistical mechanics of strategic interaction[J]. Games and Economic Behavior, 1993, 5 (3) : 387 - 424.

[69] STANLEY H. Phase transitions and critical phenomena[M]. [S.l.]: Oxford University Press, 1971.

[70] YANG Y, LUO R, LI M, et al. Mean Field Multi-Agent Reinforcement Learning[C]//Proceedings of Machine Learning Research: vol.80 Proceedings of the 35th International Conference on Machine Learning. 2018 : 5571 - 5580.

[71] HU S, LEUNG C W, LEUNG H F. Modelling the dynamics of multi agent q-learning in repeated symmetric games: A Mean Field The oretic Approach[M]. Curran Associates Inc., 2019.

[72] SUBRAMANIAN J, MAHAJAN A. Reinforcement learning in stationary mean-field games[C]//AAMAS '19: Proceedings of the 18th International Conference on Autonomous Agent s and Multi AgentSystems. [S.l.]: International Foundation for Autonomous Agent s and Multi Agent Systems, 2019 : 251 - 259.

[73] YANG K, GULER S, MENENDEZ M. Isolated intersection control for various levels of vehicle technology: Conventional, connected, and automated vehicles[J/OL]. Transportation Research Part C: Emerging Technologies, 2016, 72 : 109 - 129.

[74] LEE J, PARK B B, YUN I. Cumulative travel-time responsive real-time intersection control algorithm in the connected vehicle environment[J]. Journal of Transportation Engineering-asce, 2013, 139 : 1020 - 1029.

[75] GULER S I, MENÉNDEZ M, MEIER L. Using connected vehicle technology to improve the efffficiency of intersections[J].Transportation Research Part C: emerging Technologies, 2014, 46 : 121 - 131.

[76] FENG Y, HEAD K L, KHOSHMAGHAM S, et al. A real-time adaptive signal control in a connected vehicle environment[J/OL]. Transportation Research Part C: Emerging Technologies, 2015, 55 : 460 - 473.

[77] LI W, BAN X. Connected vehicles based traffffic signal timing optimization[J/OL]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20 (12) : 4354 - 4366.

[78] XU B, BAN X J, BIAN Y, et al. Cooperative method of traffffic signal optimization and speed control of connected vehicles at isolated intersections[J/OL]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20 (4) : 1390 -1403.

[79] GUO Q, LI L, (Jeff) Ban X. Urban traffffic signal control with connected and automated vehicles: A survey[J/OL]. Transportation Research Part C: Emerging Technologies, 2019, 101 : 313 - 334.

[80] AHN K, RAKHA H A, PARK S. Ecodrive application: Algorithmic development and preliminary testing[J/OL]. Transportation Research Record, 2013, 2341 (1) : 1 - 11.

[81] WANG M, DAAMEN W, HOOGENDOORN S P, et al. Rolling horizon control framework for driver assistance systems. part i: Mathematical formulation and non-cooperative systems[J/OL]. Transportation Research Part C: Emerging Technologies, 2014, 40 : 271 - 289.

[82] WANG M, DAAMEN W, HOOGENDOORN S P, et al. Rolling horizon control framework for driver assistance systems. part ii: Cooperative sensing and cooperative control[J/OL]. Transportation Research Part C: Emerging Technologies, 2014, 40 : 290 - 311.

[83] ASADI B, VAHIDI A. Predictive cruise control: Utilizing upcoming traffffic signal information for improving fuel economy and reducing trip time[J/OL]. IEEE Transactions on Control Systems Technology, 2011, 19 (3) : 707 - 714.

[84] KAMAL M A S, MUKAI M, MURATA J, et al. Model predictive control of vehicles on urban roads for improved fuel economy[J/OL]. IEEE Transactions on Control Systems Technology, 2013, 21 (3) : 831 - 841.

[85] MAHLER G, VAHIDI A. An optimal velocity-planning scheme for vehicle energy efffficiency through probabilistic prediction of traffffic-signal timing[J/OL]. IEEE Transactions on Intelligent Transportation Sys- tems, 2014, 15 (6) : 2516 - 2523.

[86] OZATAY E, ONORI S, WOLLAEGER J, et al. Cloud-based velocity profile optimization for everyday driving: A dynamic programming- based solution[J/OL]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15 (6) : 2491 - 2505.

[87] HE X, LIU H X, LIU X. Optimal vehicle speed trajectory on a signalized arterial with consideration of queue[J/OL]. Transportation Research Part C: Emerging Technologies, 2015, 61 : 106 - 120.

[88] WU X, HE X, YU G, et al. Energy-optimal speed control for electric vehicles on signalized arterials[J/OL]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16 (5) : 2786 - 2796.

[89] OZATAY E, OZGUNER U, ONORI S, et al. Dynamic systems and control conference: Volume 1: Adaptive control; advanced vehicle propulsion systems; aerospace systems; autonomous systems; battery modeling; biochemical systems; control over networks; control systems design; cooperative and decentralized control; dynamic system modeling; dynamical modeling and diagnostics in biomedical systems; dynamics and control in medicine and biology; estimation and fault detection; estimation and fault detection for vehicle applications; fluid power systems; human assistive systems and wearable robots; human-in-the-loop systems; intelligent transportation systems; learning control analytical solution to the minimum fuel consumption optimization problem with the existence of a traffffic light[C]. [S.l.: s.n.], 2012 : 837 - 846.

[90] WAN N, VAHIDI A, LUCKOW A. Optimal speed advisory for con- nected vehicles in arterial roads and the impact on mixed traffffic[J]. Transportation Research Part C: Emerging Technologies, 2016, 69 : 548 - 563.

[91] ZHOU F, LI X P, MA J Q. Parsimonious shooting heuristic for trajectory design of connected automated traffic part I: Theoretical analysis with generalized time geography[J].Transportation Research Part B: Methodological, 2017, 95 : 394 - 420.

[92] LI Z, ELEFTERIADOU L, RANKA S. Signal control optimization for automated vehicles at isolated signalized intersections[J].Transporta- tion Research Part C: Emerging Technologies, 2014, 49 : 1 - 18.

[93] POURMEHRAB M, ELEFTERIADOU L, RANKA S, et al. Optimizing signalized intersections performance under conventional and automated vehicles traffffic[J/OL]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21 (7) : 2864 - 2873.

[94] FENG Y, YU C, LIU H X. Spatiotemporal intersection control in a connected and automated vehicle environment[J/OL]. Transportation Research Part C: Emerging Technologies, 2018, 89 : 364 - 383.

[95] YU C, FENG Y, LIU H X, et al. Integrated optimization of traffffic signals and vehicle trajectories at isolated urban intersections[J/OL]. Transportation Research Part B: Methodological, 2018, 112 : 89 - 112.

[96] SOLEIMANIAMIRI S, GHIASI A, LI X, et al. An analytical optimization approach to the joint trajectory and signal optimization problem for connected automated vehicles[J/OL]. Transportation Research Part C: Emerging Technologies, 2020, 120 : 102759.

摘自《自动化博览》2022年12月刊