云南工商学院智能科学与工程学院苏为斌

1　引言

工业六轴机械臂在生产环境中偶发碰撞事故，可能对机器人本体、周边设备和人员造成损害。随着智能制造产业的快速发展，国内外有关机器人误伤人类的报道屡见不鲜。为减少这类事故，通常采用栅栏将人员分隔开来。然而传统的安全措施不足以应对所有场景，尤其是在人机协作环境中，人类需要在没有完全隔离的情况下与机器人共同工作，故需要采取更加先进的技术来确保安全性。

智能技术的引入是一种有效的方法。该方法通过提高机器人空间运动的智能化水平，识别和绕开障碍物，有效提高了安全性。然而，长期以来学术界在研究人工智能（artificial Intelligence，AI）时，通常将智能与大脑的思考能力紧密联系在一起，过多强调算法和算力，常常忽视了具身场景对智能的影响。在实际的生产环境中，智能不仅仅是逻辑推理、数据处理和算法计算的结果，它还涉及到机器人本体在环境中的互动以及由此产生的感知和行为。“具身智能”（embodied Intelligence，EI）要求机器人本体对外界的感知更加类似于人类，而非毫无知觉的钢铁。事实上，人类的思维过程和认知功能是根植于身体结构及其与外界交互的动态调整方式之中的。人类的身体，包括感官、运动系统、神经系统等，在促进人类理解世界、展现人类技能以及解决问题方面起着至关重要的作用。若把这种先进的技术应用到工业机器人中，将极大地提高其智能化和安全化水平。

本文基于边缘计算，以工业六轴机械臂为对象，拟在肘、腕、轴等位置安装多个先进传感器，融合多传感信息，动态捕捉机械臂及末端执行器的三维可达空间（reachable space）、灵巧工作空间（dexterouswork space）和奇异位形（singular configurations）等位置信息，构建齐次空间变换坐标矩阵，动态感知障碍物和人所处的空间位置信息，并基于这些信息，以边缘计算为基础平台，研究和开发能够灵活避障的具身智算工具，以期促进机械臂智能化和安全化水平的提升。

2　相关研究

EI的概念最早可追溯到1950年，艾伦·图灵^[1]探讨了AI发展的两条路径：一条是聚焦于抽象计算所需的智能，另一条则是为机器配备传感器和执行器，使其能够与环境互动并进行学习。1986年，布鲁克斯^[2]提出了行为式机器人概念，强调智能是具身化和情境化的体现。2000年左右，罗尔夫·普费弗和克里斯蒂安·谢尔^[3]提出智能是行为主体基于整个身体结构和功能的综合体现。近年来，随着强化学习技术的快速发展，EI在机器人控制领域得到了广泛的应用。申铠瑶、聂一鸣等^[4]对比了传统比例积分微分、滑动模态控制等方法，综述了基于图神经网络和Transformer的EI形态控制方法。陈铂垒、钟萍等^[5]从计算机视觉识别出发综述了以物体目标导航为导向的EI架构。北航任磊团队^[6]则把EI提升到了推动智能制造产业发展，并把EI认为是AI的终极表现形式。

可见，EI已再度成为当前AI领域的研究热点。由于EI强调智能体通过身体与环境的互动产生智能行为，因此需要强大的计算资源来实时处理感知数据、生成交互指令以及执行复杂任务，边缘计算显然是EI的最佳支持平台。然而当笔者以“边缘计算、具身智能”作为关键词检索国内外研究文献时，发现现关研究太少，且这些仅有的文献大多集中发表于2024年。比如基于云计算与雾计算相互融合的EI框架^[7]，以及基于斯坦福大学开源机器人ROS框架融合YoloV5的EI控制方法^[8]。在国内，邓三鹏等^[9]提出了EI机器人研究存在的问题，并给出了相关建议，然而其文章更加倾向于应用AI大模型及深度学习加强EI研究，对于计算平台则没有更多阐述。

尽管EI与边缘计算结合具有重要的实践意义，但目前相关研究和应用相对较少，且尚处于起步阶段，缺乏系统深入的开发。因此本文以六轴机械臂为实践对象，以边缘计算为平台，提出了一种新型的具身智算平台。

3　理论分析

六轴机械臂的各个关节旋转决定了末端执行器在三维空间中的位置和姿态变化。为了将这些关节的旋转运动转换为笛卡尔坐标系中的位置和姿态，通常使用正向运动学和逆向运动学来进行计算。

3.1　轴关节运动关系

六轴旋转关系如表1所示。

表1 六轴机械臂轴关节运动方向

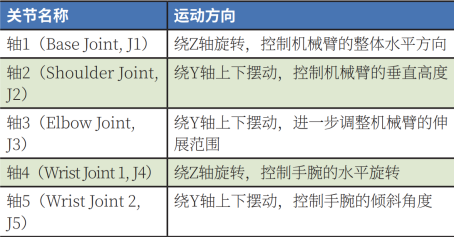
3.2　正向运动学与解逆

正向运动学是从给定的关节旋转角度计算末端执行器在笛卡尔坐标系中的位置和姿态。其具体步骤如下：

（1）齐次变换矩阵：每个关节的旋转可以表示为一个齐次变换矩阵，该矩阵描述了从一个坐标系到另一个坐标系的变换。假设每个关节旋转相应角度，则每个关节的变换矩阵Ti可以简写表示为式（1）：

其中：

R_i是3×3旋转矩阵，描述了坐标系之间的旋转关系。

p_i是1×3平移位置矩阵，描述了坐标系之间的位移关系。

0是1×3全零矩阵，1是比例变换标量，两者用于保持齐次坐标的形式。

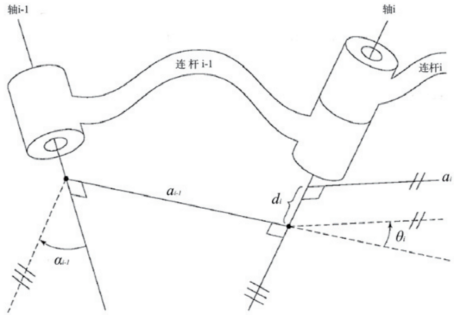
图1 机械臂的四个D-H参数

这种参数化的方法是由法国工程师雅克·丹纳维特（Jacques Denavit）和理查德·哈滕贝格（Richard S.Hartenberg）于1955年提出，简称D-H参数^[10]。R_i旋转矩阵和p_i位置矩阵由机械臂X轴向连杆长度a_i、关节轴线扭角α_i、Z轴向偏距d_i和沿Z轴旋转偏离X轴的连杆夹角θ_i构成，其几何关系如图1所示。由于六轴机械臂各连杆与轴都呈现为垂直关系，则相对坐标系与参考坐标系在递推构造T_i时可写成式（2）：

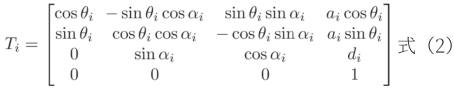
若从机械臂基座开始推导，其变换矩阵T₁是相对于J₁到J₂计算而得，X轴和Z轴平移了一个固定数量，所以a₁、d₁是一个常数，J₂关节与J₁关节扭转了π/2，J₂旋转产生在局部坐标相对于X轴的连杆夹角θ₁是一个变量，如表2所示。

接着，从J₂到末端执行器可以依次推导出变换矩阵T₂～T₆所对应的D-H参数，需要注意的是T₆是末端执行器的连接法兰，其每个关节定义的相对座标如图2所示。

表2 六轴机械臂变换矩阵D-H参数

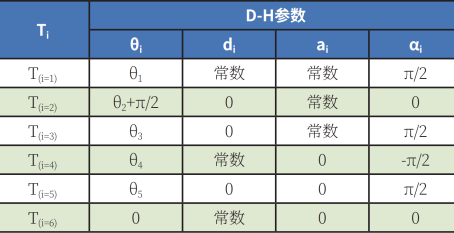
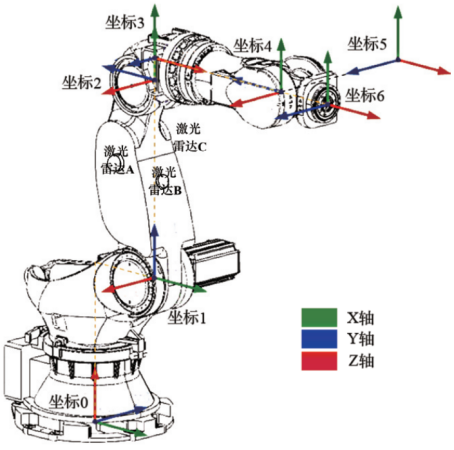
图2 六机械臂关节坐标定义

（2）串联变换矩阵：为了得到末端执行器相对于基座的总变换矩阵T_end，需要将所有关节的变换矩阵依次相乘，如式（3）：

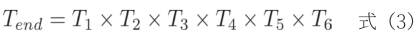
最终的变换矩阵T_end包含了末端执行器在笛卡尔坐标系中的位置p_end和姿态R_end信息，可提取出欧拉角（euler angles）、四元数（quaternion）或旋转矩阵等形式，用于描述末端执行器的姿态。其运算后的矩阵形式表示如式（4）：

（3）解逆的增强方法：逆向运动学是从已知末端执行器在笛卡尔坐标系中的位置和姿态，计算出各个关节的角度，计算复杂，且存在多个解或无解的情况。在EI与边缘计算赋能的架构下，可以通过传感器感知机械臂各个关节和障碍物所处空间位置。如图2所示，在机械臂肘部安装3个小型固态激光雷达，通过边缘算力解析点云数据便能实现。当然构建EI赋能的传感器并不限于激光雷达，也可以使用其它触觉、听觉、视觉、红外等高级传感器。

3.3　空间矩阵融合算法

将激光雷达（LiDAR）的空间矩阵进行融合，可以显著提高环境感知的精度和可靠性，但通常需要解决以下几个关键问题：坐标系对齐、数据同步、点云配准和融合算法。

（1）坐标系对齐：3个激光雷达的空间位置不同，因此首先需要进行外参标定，以确定它们之间的相对位置。由于3个雷达均安装于机械臂肘上，具有已知几何形状，故可采用静态标定板法如棋盘格或平面板^[11]，其优点是结构简单，对边缘算力的要求不高。

（2）坐标系转换：当激光雷达的相对位姿确定后，就可以使用齐次变换矩阵将每个激光雷达的点云数据转换到一个统一的坐标系中。令激光雷达B为参考坐标系，则肘部两侧的A和C相对于B的变换矩阵分别为TBA和TBC，对于点云矩阵，应考虑A、C雷达镜像安装关系及与B的垂直关系。假设变换后，激光雷达A和C的点云数据为PA和PC，则可以通过式（5）转换到激光雷达B的坐标系中：

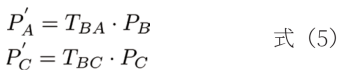
经过齐次变换后，PA(’)、PC(’)和P_B三个坐标的点云数据便可处于共同的三维空间。但此时三个雷达数据的视场角会产生数据重叠以及因比例和位置失调造成的偏差，可在机械臂上定义三个绝对物理参考点，且让三个雷达均扫描到这些点。最后通过绝对角度和距离作为系数进行配准，便可修正三个雷达的比例和位置失调。

（3）加权融合：对于三个雷达的视场角有重叠的情况，根据每个雷达的测量精度和置信度，对重叠区域的点云进行加权平均。通常，距离越近、反射率越高、测量误差越小的点权重越大。因三个雷达的累加权重未必为1，故加权平均公式为式（6）：

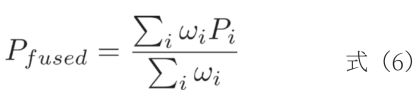
4　系统框架

在完成理论分析后，便可在该理论基础上搭建系统框架。众所周知，边缘计算将业务下沉到靠近控制对象一侧，降低了网络延迟，提高了实时性，故可不用过度依赖遥远的云计算资源，提高了系统的可靠性和稳定性。这种方式不但为EI提供了及时、高效的算力，而且还为接入各类传感器提供了泛在的接口。因此边缘计算是六轴机械臂实现智能化突破的最佳平台。本文提出的系统框架如图3所示。

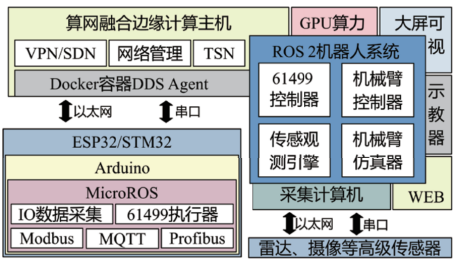
图3 六轴机械臂具身智算平台系统框架

该六轴机械臂的EI控制平台采用ROS2开源操作系统为核心，是一种构建于多台计算机之上的元操作系统^[12]。本框架给出了六种计算机，分别是算网融合主机、GPU算力主机、数据可视化主机、机器人示教器编程主机、WEB服务器和高级传感器采集计算机。其中，算网融合主机既是路由器，用于负责连接各台主机、保障网络安全和管理网络地址，又是虚拟网络VPN/SDN和时间敏感网络TSN的管控中心，还是嵌入式采集器的代理容器，是上下层系统无缝连接的关键环节。

由ESP32或STM32开发的嵌入式控制器，在Arduino框架之上通过集成MicroROS，负责模拟量和开关量的数据采集与输出控制。IEC61499实现了嵌入式端与ROS2内核的映射，并开发了常用工业通信协议如Modbus、Profibus和物联网MQTT通信等。

ROS2把所有涉及六轴机械臂的计算单元无缝关联到了一起，使原本分离的计算机变成了一个整体。在ROS2之上开发的机器人节点分布在最合适的计算机上各司其职，针对机械臂开发IEC61499控制器、机械臂控制器、传感器的观测引擎和机械臂的仿真器等。

5　总结和展望

本文针对工业六轴机械臂，分析了坐标变换和坐标融合的理论方法，给出了一种针对机械臂具身智算平台的边缘计算系统框架方案。未来，将通过搭建该具身智算平台，代替六轴机械臂的传统模式，提升人机协作水平。计划在2026年完成平台建设，成功开发EI赋能的新型机械臂，显著提高智能化水平。

未来，延续本文思路，将实现一项应用场景试点。比如在搬运码垛场景，工程师只需向机器人指定任务的源头和搬运目标，接着通过口头语音、手势、图片等对工作任务进行描述，机械臂在认清所需搬运物资的形状、颜色、数量和大概尺寸信息后，便能自动选用夹具、生成导航路径和自动完成搬运、堆垛、码放等。此外，在机械臂的运动轨迹上将实时生成避障策略，防止碰撞事故发生。

作者简介：

苏为斌（1983-），男，云南通海人，副教授，博士，现任教于云南工商学院智能科学与工程学院，主要研究方向为边缘计算、工业自动化、人工智能等。

参考文献：

[1] Turing A M. Computing machinery and intelligence[M]. Springer Netherlands, 2009.

[2] Brooks R. A robust layered control system for a mobile robot[J]. IEEE journal on robotics and automation, 1986, 2 (1) : 14 - 23.

[3] Pfeifer R, Scheier C. Understanding intelligence[M]. MIT press, 2001.

[4] 申铠瑶, 聂一鸣, 商尔科, 等. 具身智能形态控制方法综述[J]. 智能安全, 2024, 3 (1) : 74 - 84.

[5] 陈铂垒, 康嘉绪, 钟萍, 等. 面向具身人工智能的物体目标导航综述[J/OL]. 软件学报, 1-43 [2025-01-06].

[6] Ren L, Dong J, Liu S, et al. Embodied Intelligence Toward Future Smart Manufacturing in the Era of AI Foundation Model[J]. IEEE/ASME Transactions on Mechatronics, 2024.

[7] Hu D, Lan D, Liu Y, et al. Embodied AI Through Cloud-Fog Computing: A Framework for Everywhere Intelligence[C]//2024 IEEE 33rd International Symposium on Industrial Electronics (ISIE). IEEE, 2024 : 1 - 4.

[8] Gan Y, Zhang B, Shao J, et al. Embodied Intelligence: Bionic Robot Controller Integrating Environment Perception, Autonomous Planning, and Motion Control[J]. IEEE Robotics and Automation Letters, 2024.

[9] 邓三鹏, 张香玲, 王凯, 等. 具身智能机器人关键技术及发展趋势研究[J]. 装备制造技术, 2024, (6) : 2 - 10.

[10] Denavit J, Hartenberg R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. Journal of Applied Mechanics, 1955, 22 (2) : 215 - 221.

[11] Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on pattern analysis and machine intelligence, 2000, 22 (11) : 1330 - 1334.

[12] 苏为斌. 论边缘计算元操作系统[J]. 自动化博览, 2024, 41 (2) : 59 - 63.

摘自《自动化博览》2025年2月刊