摘要：非侵入式负荷监测是自动化设备用电安全监测的重要技术。针对常用电器存在功率值接近导致负荷分解准确率低的问题，原有基于低频数据的方法无法对其有效分解，本文提出了一种基于SV-ISSA（Improved Sparrow Search Algorithm）的非侵入式负荷分解方法。基于事件检测后得到的功率波形，使用DTW算法提取电器的典型功率矩阵，利用改进层次聚类算法将功率矩阵转换为状态向量，并利用滑动窗口提取电器超状态，对超状态进行缩减并获取其对应功率矩阵。此时负荷分解问题可转换为求解最优组合问题，然后通过改进的麻雀搜索算法求解各个电器超状态的运行状况，从而得到最终分解结果。实验结果表明，采用所提方法可有效提高负荷分解准确率，且能够准确处理具有相似功率范围同时运行的多种电器。

关键词：SV-ISSA；状态向量；超状态；功率矩阵；改进麻雀搜索算法；低频数据；

1 引言

随着电网信息化、自动化、智能化进程加快，电力系统对需求侧的透明度要求越来越高，实时、精确的负荷设备识别对于电力系统的规划、负荷预测以及市场调节至关重要。从目前情况来看，负荷监测与用能分析具有广阔的发展前景，通过负荷监测与用能分析可以为居民用户提供详实的家庭能效信息，也能预测用户的用电消耗，帮助用户分析家庭能耗构成，使用户了解自身行为习惯对于家庭能效的影响，从而引导用户自觉采取节能措施，并养成节能行为习惯，同时为用户提供个性化的用电设备节能控制策略服务。

1992年，Hart^[1]首次提出非侵入式负荷监测（non-intrusive load monitoring，NILM）这一概念。目前，负荷分解的模型及算法主要分为两大类：一类是模式识别算法，即直接从负荷数据中学习负荷的特征模式，建立负荷特征库，然后提取未知负荷的特征模式，逐一与负荷特征库中的负荷特征模式进行匹配，如k近邻（knearest neighbor, KNN）^[2-4]、决策树^[5-7]、支持向量机（Support vector machine，SVM）^[8-11]、神经网络（neural network,ANN）^[12-15]等都是在负荷辨识中常用的模型。第二类是优化算法，通过选取具有线性叠加性的负荷特征量，将观察到的负荷特征测量值与负荷特征库中负荷特征信号的可能组合进行匹配，以减少匹配误差作为优化目标，利用优化算法求解负荷最优化组合问题，如粒子群算法^[16-17]、整数规划算法^[18-20]、差分进化算法^[21-22]。这类方法仅在一定条件下可识别出同时工作的多种负荷，同时传统数学优化算法在寻优过程时间长，对初值的要求较高；现在的群体智能算法原理简单，容易实现，搜索能力较强，但容易陷入局部最优，因此在智能算法的选择和改进中应注意提高算法的全局寻优能力。

基于上述分析，本文提出了一种基于SV-ISSA的非侵入式负荷分解方法。选取负荷稳定工作时的功率序列，提取其状态向量所对应的功率矩阵作为负荷特征量，其反映了每种电器独特的运行模式，然后将此应用于改进麻雀搜索算法的适应度函数，从而实现了更高的非侵入式负荷分解准确率。

2 负荷分解模型

2.1 负荷特征的提取

不同设备具有不同的运行模式，其功率曲线具有一定的独特性。通过提取电器周期运行波形，对提取的波形使用动态时间规划（DTW）算法计算其相似度，来获取电器的典型波形。使用DTW算法去除重复波形，将训练集中出现的剩余波形作为典型波形，此方法假定训练集中存在各电器所有的典型波形。

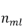通过DTW算法得到电器的功率矩阵为，式中，为电器m提取的功率矩阵长度，P为有功功率，Q为无功功率。

对于电器的典型功率数据，使用聚类获得该电器的工作状态。本文主要使用的为改进凝聚层次聚类，此方法不需要指定聚类中心数量，只需设定聚类终止条件便可达到所需结果，经过聚类后得到每种电器的状态向量，如电器m状态向量表示如下：

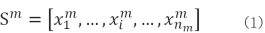
式中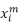：为电器m在i时刻的工作状态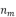；为电器m状态向量的长度，其中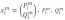，为状态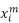对应的有功功率值与无功功率值，即为状态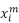所属集群的集群中心。

2.2 建立优化模型

如图1所示，以w为窗口长度，一个采样点为步长，在电器状态向量S上滑动，提取长度为w的状态向量，将此状态向量定义为超状态。

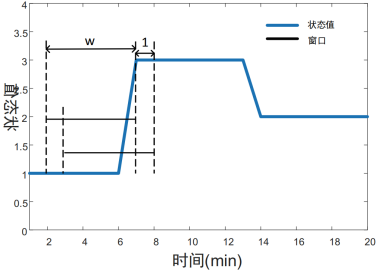
图1 超状态提取流程

如下，得到各电器的超状态，表示为：

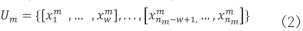
所得到的超状态存在一定的重复性，故需对重复的超状态进行缩减。缩减方式借用凝聚层次聚类中邻近度的思想，计算两两超状态之间的邻近度，构建邻近度矩阵，当两超状态之间邻近度大小为0时，对此两超状态取其一。

缩减后得到如下结果：

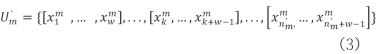
式中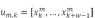：表示电器m当前处于超状态。

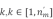缩减后的超状态对应的功率矩阵如下：

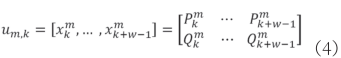
假定某一家庭中有M种电器，根据稳态功率的线性叠加性可知，采集到的家庭总功率近似等于M种电器功率的线性叠加，即

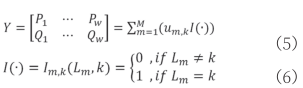
式中：Y为总功率矩阵,I(·)为指示函数，L_m表征电器m当前处于的超状态，。

本文使用待测的功率矩阵与式（7）中的功率矩阵之间欧氏距离最小建立目标函数，从待测的总功率序列中，截取长度为w的功率矩阵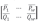，即目标函数为

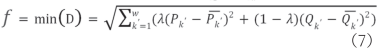
式中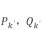：由式（7）获取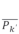，为待分解功率矩阵中第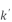列对应的有功功率值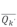，为待分解功率矩阵中第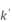列对应的无功功率值，λ为有功功率所占权重。

通过改进麻雀搜索算法求得最优解，使得适应度值f取得最小，此时便可得到各电器处于何种超状态。

3 改进麻雀搜索算法

标准麻雀搜索算法^[23]作为一种新提出的优化算法，它具有局部搜索能力极强，收敛速度较快的优点，但其容易陷入局部最优，同时全局搜索能力较差。故本文对麻雀搜索算法进行一定改进，作为改进麻雀搜索算法（Improved Sparrow Search Algorithm, ISSA）将之应用于上面模型的求解。通过对SSA研究发现，当R₂<ST时，其发现者位置更新方式存在一定的跳跃性，导致发现者在飞行行为中的搜索策略较差，故对此进行改进。

改进后的发现者位置更新公式如下：

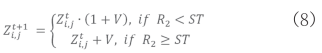
式中：t为当前迭代次数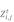，为种群中第t代中第i个个体的第j维位置，j=1,2,...,d,d为待优化问题变量的维数，R₂和ST分别为预警值和安全值，其中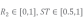,V为服从正态分布的随机数。

同时，SSA中的跟随者在全维度向目前最优位置靠近，此方法能够达到快速收敛的效果，但容易陷入局部最优，故对跟随者位置更新方式作如下改进:

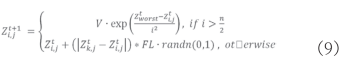
式中：Z_worst为当前全局最差的位置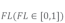，表示为跟随者随同发现者的概率，randn(0,1)代表服从期望值为0，标准差为1的高斯分布的一个随机数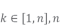；为种群数，此式中，跟随者以一定概率向发现者靠近，有效地跳出了局部最优。

分解的总流程如图2所示。

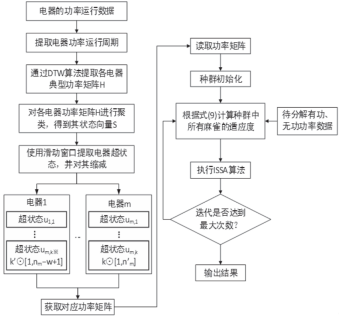
图2 基于SV-ISSA的NILM方法流程图

4 实验与讨论

4.1 评价指标

自非侵入式负荷分解概念提及以来，国内外对于这一问题提出了许多的评价指标，不同的评价指标适合的研究方法也不相同，本文采用了两种指标评价算法分解的准确率：状态估计准确率、功率分解准确率。

（1）状态识别准确率^[24]

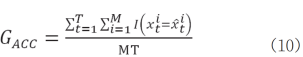
式中：为估计值；M为电器数，T为序列长度。状态识别准确率用于评价算法对各个时刻电器工作状态的识别是否准确。

（2）功率分解准确率^[25]

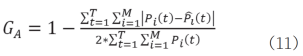
式中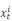，为t时刻第i个电器的实际有功功率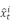，为t时刻第i个电器的估计有功功率。功率分解准确率用于计算各个时刻各电器工作功率的分解结果与实际功率的偏差大小。

4.2 实验算例

本文选择2013年西蒙弗雷泽大学发布的AMPds数据集^[26]与实测数据进行测试验证，其中AMPds数据集包含了加拿大一个家庭一年的电表监控数据，以一分钟的采样速度记录一所房屋的能耗。根据现代家庭生活中电器的普及程度以及出现频率，选取AMPds数据集中的热泵、冰箱、空调、照明灯和洗碗机作为算例验证对象。在AMPds数据集中，选择十天数据作为训练集，主要提取电器功率典型波形，后三天数据作为测试集。根据各种电器的运行周期特征，采集各个电器典型功率波形构成特征集，其中热泵298min，冰箱98min，空调278min，照明灯250min，洗碗机289min，如图3所示。通过大量实验数据得到，窗口长度w设置为11，有功功率所占权重λ=0.2时所得到的分解结果最优。改进麻雀搜索算法优化参数设置如下：种群规模为40，发现者比例为0.7，预警者比例为0.2，安全值为0.6，最大迭代次数为200。

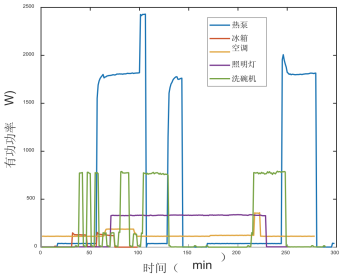
图3 电器功率变化曲线

4.3 实验结果

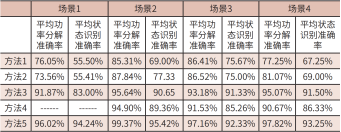
为了验证所提出方法的性能，对以下事例进行验证，在给定的后三天数据集中随机选取各电器十组长度为60min的功率序列作为测试集。对7种不同负荷组成四种场景各进行20次仿真实验，场景一：电磁炉与电热水壶同时运行，场景二：冰箱与空调运行，场景三：热泵、冰箱、空调同时运行，场景四：热泵、空调、照明灯、洗碗机同时运行。在实验中，方法1是以单点构造适应度函数的离散粒子群优化算法，方法2是以单点构造适应度函数的改进麻雀搜索算法，方法3是以本文特征矩阵构造适应度函数的离散粒子群优化算法。方法4为文献[27]算法，方法5是为本文算法。由于方法4需要获得电器运行时间概率分布，而本文中场景二所用电器为实测数据，无法准确得到其时间概率分布，故此场景中方法4未实施。

由表1可知，功率较大的电器识别率较高，功率较小的电器，识别精度会降低，当同一电器不同状态对应的功率范围差距较小时，会造成状态识别精度降低，如空调中存在两种状态其对应功率均值分别为108W和114W，当与大功率电器同时运行时，会降低其状态识别准确率。

通过比较将单点有功功率、无功功率作为特征与本文特征可知，对于低功率、相似功率电器，本文具有更高的识别效果。

表1 几种电器分解准确率

4.4 不同长度窗口的影响

在本节中，我们评估不同窗口长度对负荷分解准确率的影响，计算四种电器在不同窗口长度下的平均分解精度，如图4所示。

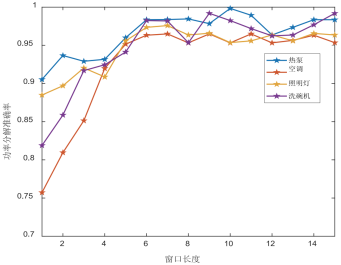
图4 不同窗口长度下的平均分解精度

由图4可知，随着窗口的增大，其功率分解率随之增大，当获取到足够多的特征时，功率分解率达到最大值并趋于稳定，但由于窗口长度的增加，其提取的电器超状态数增加，导致求解时间变长，同时，考虑到电器在运行期间存在功率曲线失真的可能性，窗口的长度应小于每个电器的最小运行周期，为保持算法的性能下减少计算成本，将窗口长度选择为w=11。

4.5 算法的收敛度分析

由图5可以看出，标准麻雀搜索算法可能陷入局部最优解，从而停止搜索，得不到全局最优解。而在改进麻雀搜索算法中，改进发现者位置更新方式的同时改进警戒者位置更新方式，从而使麻雀向最优解方向进行搜索，而不是直接跳跃到最优解附近，提高该算法的全局搜索能力。当标准算法寻得局部最优解，未能正确识别电器运行状态；而改进麻雀搜索算法在寻得此局部最优解后仍继续寻优搜索，最终求得全局最优解，准确识别出当前电器种类及其运行状态。

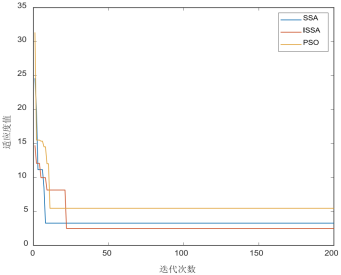
图5 三种算法适应度收敛曲线

同时，本文随机抽取了6分钟的负荷数据，使用离散粒子群算法与改进麻雀搜索算法计算20次，两种算法迭代次数都设置为200，其单次求解平均准确度和计算时间如表2所示。

表2 两种算法求解能力

由表5可知，本文算法相对于粒子群算法来说，具有更好的寻优能力，同时，其计算时间大幅减少。

5 结论

为了提高相似负荷分解准确度，本文提出了一种基于SV-ISSA的非侵入式负荷分解方法，利用电器的状态向量及其对应的功率矩阵作为特征量，以总功率序列与模板序列之间距离最小为目标建立负荷分解模型，使用改进麻雀搜索算法对此模型求解。实验表明该模型对典型电器的功率分解率达到94%以上，对于小功率电器，由于特征不明显，分解率会逐渐降低。提出的方法可以分解功率大小相似的多种负荷，还能有效分解功率差值较大的负荷组合，同时，此方法所需的硬件和软件需求少，采样频率要求低。但本文仍存在一定的局限性，在特征提取阶段，需要准确获得电器运行的典型波形，同时，针对小功率负荷准确率较低的情况，在下一步的研究中将会着力解决分解过程中大功率负荷对小功率负荷分解的影响。

★基金项目：杭州电力设备制造有限公司科技项目（YF211601）。

作者简介：

叶超（1987-），男，浙江建德人，工程师，现就职于杭州电力设备制造有限公司桐庐白云源成套电气制造分公司，主要从事电气设计研发工作。

参考文献：

[1] Hart G W. Nonintrusive appliance load monitoring[J]. Proceedings of the IEEE, 80 (12) : 1870 - 1891, 1992.

[2] Figueiredo M., A. D. Almeida & B. Ribeiro. "Home electrical signal decomposition for non-intrusive load monitoring (NILM) systems[J]. Neurocomputing, 2012 : 66 - 73.

[3] Chuan Choong Yang, Chit Siang Soh & VooiVoon Yap. A systematic approach in appliance decomposition using k-nearest neighbours and naive Bayes classifiers for energy efficiency[J]. Energy Efficiency, 2018 : 518 - 529.

[4] Chuan Choong Yang, "A systematic approach in load decomposition utilizing a multi-stage classification algorithm for consumer electrical appliances classification[J]. Frontiers in Energy, 2019, 13 (2) : 386 - 398.

[5] Nguyen, M. A novel feature extraction and classification algorithm based on power components using single-point monitoring for NILM[J]. Electrical & Computer Engineering IEEE, 2015 : 37 - 40.

[6] Bundit Buddhahai, A non-intrusive load monitoring system using multi-label classification approach[J]. Sustainable Cities and Society, 2018, 39 : 621 - 630.2022.11 AUTOMATION PANORAMA 77

[7] Hoyo-Montaño, José A. Non-Intrusive Electric Load identification using Wavelet Transform[J]. Ingeniería e Investigación, 2018, 38 (2) : 42 - 51.

[8] "Non-intrusive load monitoring of air conditioning using low-resolution smart meter data[C]. 2016 IEEE International Conference on Power System Technology (POWERCON) IEEE, 2016.

[9] Singh, M., Kumar, S Samwell S& Prasad, R. S. Residential Load Signature Analysis for Their Segregation Using Wavelet—SVM[J]. Power Electronics and Renewable Energy Systems, 2014, : 863 – 871.

[10] Kwok Tai Chui, Energy Sustainability in Smart Cities: Artificial Intelligence, Smart Monitoring, and Optimization of Energy Consumption[J]. Energies (2018), : 2869 - 2881.

[11] Donglin Su. Nonintrusive Load Monitoring Based on Complementary Features of Spurious Emissions[J]. Electronics 8.9 (2019), : 1002 - 1014.

[12] Chang, H. H. et al. Feature Extraction-Based Hellinger Distance Algorithm for Nonintrusive Aging Load Identification in Residential Buildings[C]. IEEE Transactions on Industry Applications 52.3 (2016) : 2031 - 2039.

[13] Yu-Hsiu Lin, and Yu-Chen Hu. Electrical Energy Management Based on a Hybrid Artificial Neural Network-Particle Swarm Optimization-Integrated Two-Stage Non-Intrusive Load Monitoring Process in Smart Homes[J]. Processes, 2018, (6) : 236 - 252.

[14] Qian, Wang, Fei. Concatenate Convolutional Neural Networks for Non-Intrusive Load Monitoring across Complex Background[J]. Energies, 2019, (12) : 1572 - 1589.

[15] Min C, Wen G, Yang Z, et al. Non-Intrusive Load Monitoring System Based on Convolution Neural Network and Adaptive Linear Programming Boosting[J]. Energies, 2019, (12) : 2882 - 2891.

[16] Ding, G. A Novel Non-intrusive Load Monitoring Method Based on Quantum Particle Swarm Optimization Algorithm[C]. 2019 11th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA) 2019, : 230 - 234.

[17] Fu, Q. Nonintrusive load monitoring based on particle swarm optimization[C]. 2019 IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia) IEEE, 2019, : 2505 - 2509.

[18] Shinkichi Inagaki. Nonintrusive appliance load monitoring based on integer programming[J]. Electrical Engineering in Japan 174.2 (2011), : 18 - 25.

[19] Wittmann, F. M., L. J. Camilo, and M. J. Rider. Non-Intrusive Load Monitoring Algorithm Using Mixed-Integer Linear Programming[C]. IEEE Transactions on Consumer Electronics 2018 : 1 - 1.

[20] Smart Grids. Findings from University of Sydney Yields New Data on Smart Grids[J]. Journal of Technology & Science, Sep. 2018.

[21] Kong W., Zhao Y D, Jin M. An Extensible Approach for Non-Intrusive Load Disaggregation with Smart Meter Data[J]. IEEE Transactions on Smart Grid, 2016, (99) : 1 - 1.

[22] Xue Jiankai, and Shen Bo. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020,8 (1) : 105358.

[23] Kim, H. Unsupervised decomposition of Low Frequency Power Measurements[C]. Eleventh Siam International Conference on Data Mining DBLP, 2012, 5.

[24] Kolter, J. Z., and M. J. Johnson. REDD: A Public Data Set for Energy decomposition Research[J]. Artificial Intelligence, 2011, 25.

[25] Makonin S, F Popowich, Bartram L. AMPds: A public dataset for load disaggregation and eco-feedback research[C] Electrical Power & Energy Conference. IEEE, 2014, 5.

[26] Yan, X. & Zhai S. & He, G. Non-intrusive Load decomposition Based on Time Probability Distribution and Super State of Appliances[J]. Dianli Xitong Zidonghua/Automation of Electric Power Systems.2018, 42 : 53 - 58 、73.

摘自《自动化博览》2022年11月刊