★田长彬，彭勃，马昕，马翔雪（山东建筑大学信息与电气工程学院，山东济南250101）

★孙玉琼（济南市云映传媒科技有限公司，山东济南250003）

摘要：为了降低岩土工程灾害造成的损失，亟需对工程结构进行实时、长期监测。以FBG（光纤布拉格光栅）为传感点，以具有防水防潮特性的POM（聚甲醛）材料为柔性基底，采用刻槽方式将传感点封装在基底中制作而成的FBG柔性传感器，经过温度传感实验，表明具有良好的温度自补偿特性。位移传感实验中，对传感点获取的曲率信息采用三次函数插值后，利用位移重建算法得到的测量点的平均相对误差分别减小0.77mm（类型1）、12.60mm（类型2）和15.53mm（类型3）。插值后每个测量点的最大相对误差百分比分别为6.38%（类型1）、7.06%（类型2）、7.08%（类型3）。表明插值算法有效提高了柔性传感器对位移的感知精度。设计制作的FBG柔性传感器可以用于岩土工程变形场的实时监测，具有重要的应用与推广价值。

关键词：岩土工程；光纤布拉格光栅；柔性基底；温度自补偿；三次函数插值；位移重建算法

1 引言

众所周知岩土工程结构，如地基、边坡、隧道和大坝等，在国民经济发展中发挥了重要作用^[1-2]。目前，由于恶劣的自然环境和较长的设计周期导致许多结构健康问题日益突出，如地基沉降、边坡失稳、隧道和大坝结构开裂和变形等^[3-4]。这些工程灾害每年都会造成不可估量的经济损失和人员伤亡。为确保工程设施安全运营，对工程结构进行实时、长期监测和自动预警是实现灾害从“被动应对”向“主动防控”变革最直接、最有效的方法。

岩土工程所处地质条件复杂、环境恶劣，工程初始阶段具有隐蔽性，因此对其进行实时监测具有一定的挑战性^[5-6]。在过去的几十年中，专家学者已经研制了一系列监测仪器用于工程结构测量。例如，针对边坡滑移、路基沉降、桥梁变形的测斜仪、电感式位移传感器、多点引伸计等；GPS技术和激光扫描技术等主要用于大坝水库的变形测量。然而，传统的岩土工程仪器存在易受潮、耐久性差、实时自动监测程度低等缺点，且大多是基于点的监测，无法满足大型工程结构的智能监测^[7]。基于光纤布拉格光栅（FBG）的传感器作为一种功能强大、高效的结构健康监测方法得到了广泛的应用。与伸长计、应变计和千分表等传统传感器相比，FBG传感器具有物理尺寸小、重量轻、不受电磁干扰（EMI）、易于安装、长期稳定性和波长多路复用等许多优点^[8-9]。近年来，基于光纤光栅的传感技术越来越受到岩土工程界的关注，在不同的研究领域中也有大量的监测研究报道。研究人员针对与岩土工程结构相关的一些关键参数，如内部温度变化、应力/应变场、垂直沉降和侧向变形等^[10-12]，研发了如FBG温度传感器、FBG应力/应变传感器、FBG倾斜传感器、FBG位移传感器等一系列FBG类传感器。这些FBG传感器实时测量工程结构的位移、应变、倾角等力学参数，进而对工程结构进行安全评估。然而大多数FBG传感器采用布点的方式监测岩土工程结构的参数，无法对结构整体的位移场进行测量和评估。

近年来，以具有防水防潮特性和弯曲性能良好的柔性材料（比如聚氨酯、聚甲醛、ABS树脂、聚氯乙烯等）为基底，将FBG传感器采用表面粘贴或刻槽粘贴两种方式与柔性材料相结合，研制的FBG柔性传感器在岩土工程位移场监测中得到广泛应用。Zhu等人^[13]采用粘贴在棒表面的准分布式FBG传感器检测应变分布,然后根据Euler-Bernoulli梁理论计算沿传感棒的位移分布。研发的新型FBG传感棒用于实时高精度监测模型大坝的内部位移。Guo等人^[14]研发了一种FBG变形传感器，其结构包括测斜仪外壳和一系列嵌入FBG传感器的柔性管。基于“梁单元”方法把FBG检测到的应变分布转化成柔性杆的变形位移。该传感器用于监测边坡的位移变形。Zheng等人^[15]基于共轭梁法建立了将应变转换为侧向位移的数学方程，设计的FBG测斜仪用于获取边坡内部位移。Pei等人^[16]根据经典的超静定梁理论设计了基于FBG的原位测斜仪，其中管段的变形与安装在钻孔中的套管相协调。原位测斜仪用于监测工程结构的变形场。

上述学者的研究成果在各自的应用领域取得了良好的表现，并推动了FBG变形传感器的发展。基于FBG传感器测量的应变信息，采用应变-位移重建算法计算柔性基底的变形，由于柔性基底的刚度远小于工程结构的刚度，因此，柔性传感器的形状即可反映工程结构的位移变形。FBG传感点的布设间隔是影响柔性传感器位移测量精度的重要因素，考虑到传感器的制作成本，本文以强度高、弯曲性能良好的POM（聚甲醛）棒为柔性基底。为了保护脆弱的FBG传感点，采用刻槽方式以100mm间隔将传感点封装在柔性基底中。为了提高柔性传感器对位移的感知精度，采用三次样条插值算法对传感点获取的曲率信息进行插值，然后采用坐标旋转拟合算法重建柔性传感器的位移变形，即可得到岩土工程结构的变形场，进而对工程结构的健康状况提供实时预警。

2  FBG柔性传感器制作及位移传感原理

2.1 传感器制作

如图1所示，FBG柔性传感器以高强度、耐腐蚀、耐高温的POM棒为柔性基底，棒长度为900mm，直径为5mm，在棒表面沿轴线方向开两个矩形凹槽（深度和宽度均为1mm），两凹槽间隔180°。采用塑料焊接技术将两支FBG传感阵列植入两列凹槽内并固定，每个阵列有9支FBG测点，相邻两测布点间距为100mm。

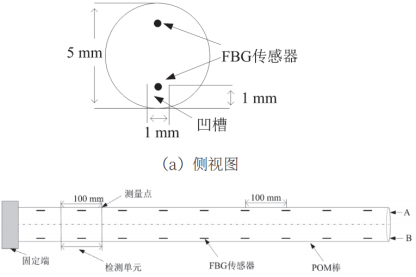
图1 FBG柔性传感器示意图

2.2 基于坐标旋转拟合算法的位移传感模型

FBG传感器的中心波长对轴向应变与温度同时敏感，其中心波长变化量Δλ、应变Δε及温度ΔT的关系为：

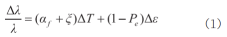
其中，λ是FBG传感器自由状态下的中心波长，α_f和ξ分别是光纤的热膨胀系数和热光系数，Pe为光弹系数，一般取值为0.22。

FBG传感器将POM棒划分为多个微段，每段作为一个检测单元，检测单元的末端为测量点。根据材料力学原理^[17]，当柔性传感器弯曲时，检测单元的曲率ρ_x为：

其中，Z是传感点与中性轴之间的距离，Δεx是传感点的应变。检测单元中布设于A、B两对称侧的传感点，当柔性传感器顺时针旋转时，传感点1受拉应变，传感点2受压应变，如图2所示。

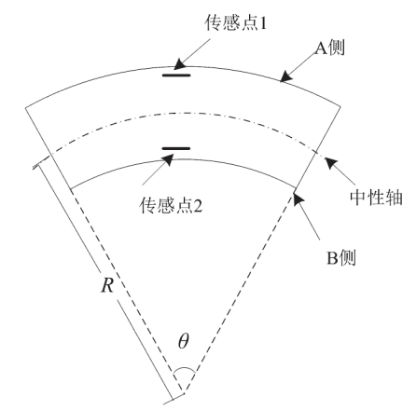
图2 检测单元测量原理示意图

由于两传感点距中性轴距离相等，由弯曲引起的两传感点波长变化大小相等方向相反，而由温度引起的两传感点波长变化方向相同。为了消除温度对传感点中心波长的影响，当检测单元发生弯曲时，检测单元的应变可以表示为：

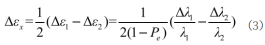
由公式（2）和（3）可知，检测单元的曲率半径R与传感点的中心波长变化量的关系为：

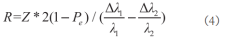
因此，通过获取传感点的中心波长变化量即可得到检测单元的曲率半径。

FBG柔性传感器可以看作是由许多检测单元组成，当柔性传感器发生弯曲时，各检测单元连续且每个检测单元曲率半径R远大于其长度L，根据微分原理，当检测单元长度足够小时，可用检测单元上传感点处的曲率代替整个检测单元的曲率，进而可以将柔性传感器视为一段连续曲线。该曲线可看作由许多微小圆弧构成，假设第i个圆弧的曲率为ρ_i-1、长度为L_i-1、起点为O_i-1、终点为O_i、半径为R_i-1、圆心角为θ_i-1（设定逆时针为正，顺时针为负）。当已知圆弧曲率和长度时，即可确定圆弧的起点和终点位置，将每个圆弧的起点和终点连接，即可得到整个曲线的形状。如图3所示，取O₀、O₁、O₂三点进行分析，令O₀为原点，在O₀处作切线为x₀轴，垂直于x₀轴为y₀轴建立坐标系。

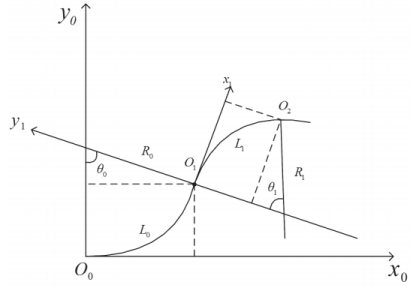
图3 坐标旋转拟合算法原理图

由于曲率和半径为倒数关系，即R₀=1/ρ₀，又因为θ₀=L₀/R₀，可得O₁坐标：

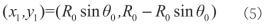
同理，在O₁处作切线为x1轴，垂直于x₁轴为y₁轴建立新的坐标系，可得O₂坐标：

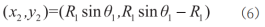
根据坐标旋转变换公式，（x₂,y₂）在x₁-O₁-y₁坐标系的坐标与在x₀-O₀-y₀坐标系的坐标有以下关系：

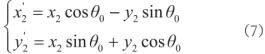
将式6代入式7可得（x₂,y₂）在x₀-O₀-y₀坐标方程。由上可得知O₁、O₂在x₀-O₀-y₀坐标系的坐标，连接两点后即可完成小圆弧的重构，以此类推可实现整个曲线拟合重建。

传感点的布设间隔是影响柔性传感器位移重建精度的重要因素，考虑到柔性传感器的制作成本，实际制作过程中传感点的布设间隔为100mm，为了提高传感器的测量精度，采用三次样条插值算法对获取的曲率信息进行插值，具体如下。

当柔性传感器发生弯曲变形时，对传感点处获取的曲率信息采用三次函数进行插值拟合，此时曲率为弧长的三次函数，对于柔性传感器上第i个传感点。

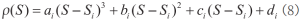
上式中，a_i、b_i、c_i、d_i是系数，ρ为检测点处的曲率，S_i是第i个检测点到初始点的距离。为保证拟合出的

曲率连续化曲线是绝对平滑的，所以一阶微分和二阶微分连续关系可知：

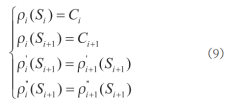
在柔性传感器实际工程应用中初始端固定，其它检测点自由，因此根据传感器首尾限制条件即可求出 a_i、b_i、c_i、d_i四个待定系数，然后根据传感器上每个插值点到初始端的距离求出该点处的曲率。三次样条插值分割点连接处的曲线光滑，受柔性传感器弯曲程度影响较小，插值效果较好。

3  实验与分析

3.1 温度实验

为了避免温度对柔性传感器测量精度的影响，首先开展温度标定实验，验证FBG柔性传感器的温度特性及自补偿效果。将柔性传感器放入恒温箱中，调节恒温箱温度从-20℃到40℃逐步升高，每次升高10℃，恒温箱温度测量精度为0.01℃，采用FBG解调仪采集传感点的中心波长，任选其中一个检测单元中两传感点的温度响应曲线，如图4所示。传感点1和传感点2分别位于柔性传感器的A、B两侧，其中心波长变化量与温度变化量的关系分别为λ₁=0.0110ΔT+0.2181，λ₂=0.0109ΔT+0.2171。因此可利用该检测单元中两传感点中心波长变化量之差实现温度自补偿。

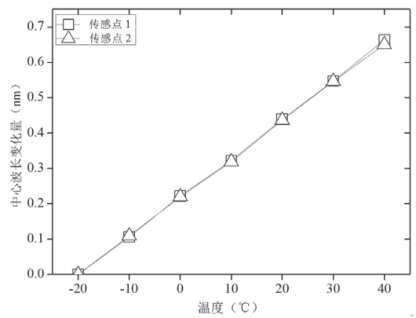
图4 两传感点的温度响应曲线

3.2 位移传感实验图4两传感点的温度响应曲线

开展FBG柔性传感器位移传感实验，实验系统的位移传感标定平台如图5所示。柔性传感器的一端固定在铺有坐标纸（单元格：mm2）的标定平台上，设B侧固定点坐标为O（0,0），B侧各测量点的坐标为P_i（100*i，0），i=1、2...9。传感器的另一端引出尾纤与解调仪相连接，解调仪解调得到的两FBG阵列的波长数据通过网线传输到电脑。在柔性传感器不同位置处施加位移使之产生不同的弯曲变形，用高精度位移传感器（精度为0.01mm）读取每个测量点的位移。

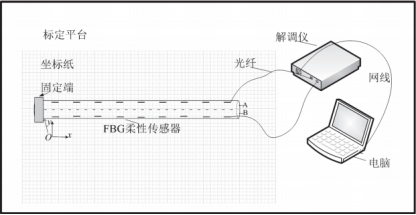
图5 位移传感标定平台

对柔性传感器三种典型的弯曲形状进行标定实验，每种弯曲类型施加6种不同大小的位移值。对于类型1：在传感器（900,0）处沿y轴方向施加六种不同大小的位移，分别为80mm、142mm、203mm、262mm、325mm、408mm；对于类型2：在坐标点（500,0）处沿y轴方向施加位移量分别为：70mm、112mm、141mm、156mm、174mm、208mm；对类型3：分别在坐标（500,0）与（900,0）两点处同时施加y轴方向的位移，六种情况下两点位移值分别为：51mm/15mm、97mm/49mm、97mm/43mm、124mm/58mm、153mm/73mm、192mm/164mm。利用解调仪采集所有传感点的中心波长，同时待位移稳定后，采用高精度位移传感器读取测量点的真实位移值。针对柔性传感器每一种弯曲类型任意选取一种位移情况，如图6所示，对传感点处曲率进行插值前后采用位移拟合算法得到的测量点位移和真实位移对比。

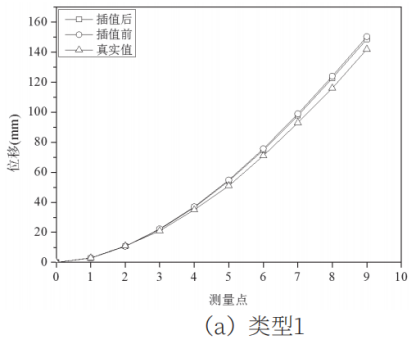
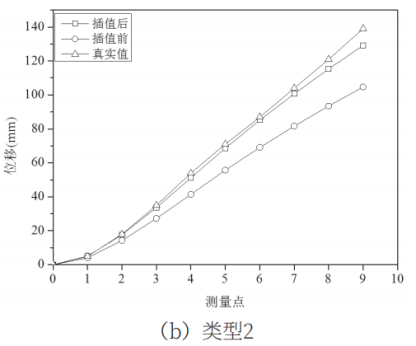
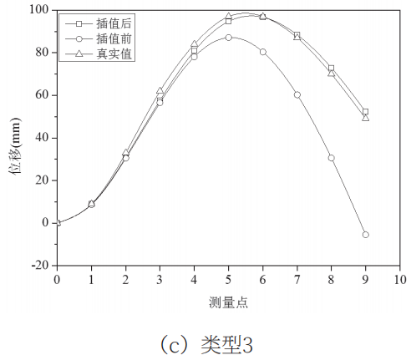
图6 不同弯曲类型下插值前后的重构位移和真实位移对比

从图6中可以看出对传感点处的曲率进行插值前重构的位移和实际测量的位移之间存在一定的误差，其中，随着测量点与固定点的距离增加，类型1，2和3相对误差逐渐增大，均是第9个测量点的相对误差最大，分别为8.40mm，34.25mm，54.53mm，可以看出，插值前重构得到的测量点的位移误差较大。而对传感点处的曲率进行插值后，三种弯曲类型测量点的误差明显减小，最大误差分别为6.64mm、9.78mm，3.30mm。

三种弯曲类型下，对传感点处的曲率进行插值前后测量点的平均相对误差如表1所示。插值后比插值前测量点的平均相对误差分别减小0.77mm、12.60mm和15.53mm。

表1 测量点的平均相对误差（mm）对比

插值后三种弯曲形状各测量点的相对误差百分比见表2。可以看出，在不同的弯曲形状下，FBG柔性传感器每个测量点的最大相对误差百分比分别为6.38%（类型1）、7.06%（类型2）、7.08%（类型3）。不同弯曲类型插值后得到的每一个测量点的相对误差百分比均较小。设计的FBG柔性传感器性能指标能够满足工程上的应用。表明对传感点处的曲率进行插值有效提高了柔性传感器对位移的感知精度。

表2 插值后各测量点（MP）的相对误差百分比（%）

4 结束语

本文以高强度、耐腐蚀、耐高温的POM棒为柔性基底，采用焊接技术将180°间隔的FBG传感阵列封装在柔性基底内部而研发的用于岩土工程变形场监测的FBG柔性传感器。温度传感实验表明，可利用每一个检测单元中两传感点中心波长变化量之差消除温度的影响，柔性传感器具有良好的温度自补偿特性。受柔性棒基体屈服强度及实验条件等因素限制，对柔性传感器的三种典型弯曲形状进行实验。实验中针对柔性传感器不同的弯曲形状，对传感点获取的曲率信息采用三次函数插值后，测量点的平均相对误差误差明显减小，和插值前相比平均相对误差分别减小0.77mm（类型1）、12.60mm（类型2）和15.53mm（类型3）。插值后每个测量点的最大相对误差百分比分别为6.38%（类型1）、7.06%（类型2）、7.08%（类型3）。表明对传感点处的曲率进行插值有效提高了柔性传感器对位移的感知精度。本文论述的FBG柔性传感器可以用于边坡、路基、桥梁等岩土工程中变形场的实时监测，具有重要的意义与应用推广价值。

★基金项目：山东省自然科学基金项目（ZR2021QD066）。

作者简介:

田长彬 （1990-），男，山东济宁人，讲师，博士，现任教于山东建筑大学信息与电气工程学院，主要研究领域为光纤传感理论及其应用。

彭 勃  （1992-），男，山东东营人，讲师，博士，现任教于山东建筑大学信息与电气工程学院，主要研究领域为新型光纤传感技术及在岩土工程的应用。

马 昕  （1987- ），男，山东济南人，讲师，博士，主要研究方向为新型光纤传感仿真建模。

马翔雪 （1991-），女，山东济南人，讲师，博士，现任教于山东建筑大学信息与电气工程学院，主要研究方向为新型光纤变形传感优化。

孙玉琼 （1990-），女，山东青岛人，工程师，硕士，现就职于济南市云映传媒科技有限公司，主要研究方向为新型光纤传感器组网配置。

参考文献：

[1] HUANG R Q. Some catastrophic landslides since the twentieth century in the southwest of China[J]. Landslides, 2009, 6 (1) : 69 - 81.

[2] HUANG D, SONG Y X, MA G W, et al. Numerical modeling of the 2008 Wenchuan earthquake-triggered Niumiangou landslide considering effects of pore-water pressure[J]. Bulletin of Engineering Geology and the Environment, 2019, 78 (7) : 4713 - 4729.

[3] CHEN F Y, WANG L, Zhang W G. Reliability assessment on stability of tunneling perpendicularly beneath an existing tunnel considering spatial variabilities of rock mass properties[J]. Tunnelling and Underground Space Technology, 2019, 88 : 276 - 289.

[4] ZENG B, HUANG D, YE S Q, et al. Triaxial extension tests on sandstone using a simple auxiliary apparatus[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 120 : 29 - 40.

[5] ZHANG D, XU Q A. BEZUIJEN G, et al. Internal deformation monitoring for centrifuge slope model with embedded FBG arrays[J] Landslides, 2017, 14 (1) : 407 - 417.

[6] PEI H F, ZHANG S Q, BORANA L, et al. Slope stability analysis based on real-time displacement measurements[J]. Measurement, 2019, 131 : 686 - 693.

[7] TIAN C B, WANG Z F, SUI Q M, et al. Design, optimization and improvement of FBG flexible sensor for slope displacement profiles measurement[J]. Sensors, 2019, 19 (17).

[8] 王彦, 金萍, 赵慧等. 基于FBG柔性传感器的形状重构[J]. 仪器仪表学报, 2021, 42 (12) : 83 - 91.

[9] 田长彬, 王静, 张峰等. 用于桥梁钢管混凝土裂缝监测的FBG传感器研究[J]. 仪表技术与传感器, 2017 (9) : 20 - 23.

[10] ZHENG Y, ZHU Z W, YI X, et al. Review and comparative study of strain-displacement conversion methods used in fiber Bragg grating-based inclinometers[J]. Measurement, 2019, 137 : 28 - 38.

[11] 孙广开, 曲道明, 闫光等. 软体气动驱动器弯曲变形光纤传感与形状重构[J]. 光学精密工程, 2019 (5) : 1052 - 1059.

[12] AMANZADEH M, AMINOSSADATI S M, KIZIL M S, et al. Recent developments in fibre optic shape sensing[J]. Measurement, 2018, 128 : 119 - 137

[13] ZHU H H, YIN J H, ZHANG L, et al. Monitoring internal displacements of a model dam using FBG sensing bars[J]. Advances in structural engineering, 2010, 13 (2) : 249 - 261.

[14] GUO Y X, ZHANG D F, FU J J, et al. Development and operation of a fiber Bragg grating based online monitoring strategy for slope deformation[J]. Sensor Review, 2015, 35 (4) : 348 - 356.

[15] ZHENG Y, ZHU Z W, DENG Q X, et al. Theoretical and experimental study on the fiber Bragg grating-based inclinometer for slope displacement monitoring[J]. Optical Fiber Technology, 2019, 49 : 28 - 36.

[16] PEI H F, CUI P, YIN J H, et al. Monitoring and warning of landslides and debris flows using an optical fiber sensor technology[J]. Journal of Mountain Science, 2011, 8 (5) : 728 - 738.

[17]GE J, JAMES A E, XU L, et al. Bidirectional soft silicone curvature sensor based on off-centered embedded fiber Bragg grating[J]. IEEE Photonics Technology Letters, 2016, 28 (20) : 2237 – 2240.

摘自《自动化博览》2022年10月刊